题目内容
若函数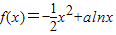
在区间（1，+∞）上是减函数，则实数a的取值范围为（ ）A．[1，+∞）
B．（1，+∞）
C．（-∞，1]
D．（-∞，1）
【答案】分析：求出f（x）的导函数，令导函数小于等于0在区间（1，+∞）上恒成立，分离出a，求出函数的最大值，求出a的范围．
解答：解：∵
∵f（x）在区间（1，+∞）上是减函数，
∴
在区间（1，+∞）上恒成立
∴a≤x2在区间（1，+∞）上恒成立
∵x2＞1
∴a≤1
故选C．
点评：解决函数的单调性已知求参数范围问题常转化为导函数大于等于（或小于等于）0恒成立；解决不等式恒成立求参数范围问题常分离参数转化为求函数的最值．
解答：解：∵
∵f（x）在区间（1，+∞）上是减函数，
∴
在区间（1，+∞）上恒成立∴a≤x2在区间（1，+∞）上恒成立
∵x2＞1
∴a≤1
故选C．
点评：解决函数的单调性已知求参数范围问题常转化为导函数大于等于（或小于等于）0恒成立；解决不等式恒成立求参数范围问题常分离参数转化为求函数的最值．
练习册系列答案
阅读快车系列答案
相关题目
在区间[－1，0]上是单调递减函数，求
的最小值；
若
，求函数
，
，若函数
在区间（-1，1）上存在单调递增区间，则t的取值范围是 ．
；
的图象；
在区间[－1，|
|－2]上单调递增，试确定
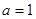时，函数
只有一个零点；
的取值范围。
在区间（1，4）内单调递减，求a的取值范围；
处取得极小值是1，求a的值，并说明在区间（1，4）内函数