题目内容
双曲线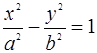
的一个焦点为
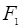，顶点为
，
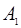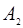，P是双曲线上任意一点，则分别以线段
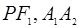为直径的两圆一定（ ）
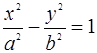的一个焦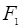点为，顶点为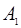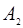，，P是双曲线上任意一点，则分别以线段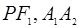为直径的两圆一定（ ）| A．相交 | B．相切 | C．相离 | D．以上情况都有可能 |
B
考点：
分析：由圆与圆的位置关系，判断两圆的位置关系需判断圆心距与半径和或差的关系，本题中圆心距即为焦点三角形的中位线，利用双曲线的定义即可证明圆心距等于半径之差，故为内切
解答：解：如图，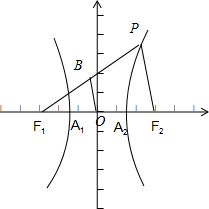
设以线段PF1，A1A2为直径的两圆的圆心坐标分别为B，O，半径分别为R，r
在三角形PF1F2中，圆心距|OB|=|PF2|/2=(|PF1|-2a)/2=|PF1|/2-a= R-r
∴分别以线段PF1，A1A2为直径的两圆一定是内切
点评：本题考查了双曲线的定义，圆与圆的位置关系及其判断，恰当的将双曲线定义与半径和、差联系起来，是解决本题的关键
分析：由圆与圆的位置关系，判断两圆的位置关系需判断圆心距与半径和或差的关系，本题中圆心距即为焦点三角形的中位线，利用双曲线的定义即可证明圆心距等于半径之差，故为内切
解答：解：如图，
设以线段PF1，A1A2为直径的两圆的圆心坐标分别为B，O，半径分别为R，r在三角形PF1F2中，圆心距|OB|=|PF2|/2=(|PF1|-2a)/2=|PF1|/2-a= R-r
∴分别以线段PF1，A1A2为直径的两圆一定是内切
点评：本题考查了双曲线的定义，圆与圆的位置关系及其判断，恰当的将双曲线定义与半径和、差联系起来，是解决本题的关键
练习册系列答案
相关题目
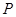是双曲线
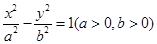与圆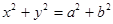
在第一象限的交点，其中
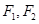分别是双曲线的左、右焦点，且
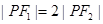，则双曲线的离心率为（ ）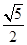
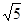
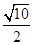
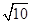
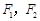分别是双曲线
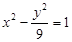的左、右焦点．若点
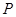在双曲线上，且
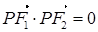，则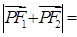
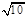
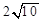
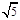
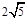
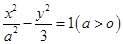的离心率为2，则 
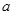等于（ *** ）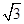
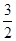
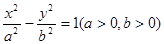的离心率为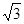
，且它的一条准线与抛物线
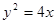的准线重合，则此双曲线的方程为 （ ）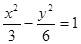
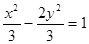
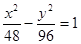
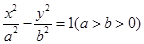，它的一个顶点到一条渐近线的距离为
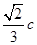（c为双曲线的半焦距长），则双曲线的离心率为 （ ）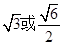
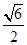
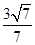
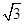
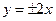，且过点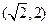
，则此双曲线的标准方程为 ．
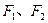分别为双曲线
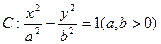的左右焦点，
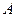为双曲线的左顶点，以
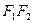为直径的圆交双曲线某条渐近线于
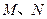两点，且满足
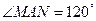．则该双曲线的离心率为 
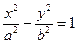(a>0, b>0)的一个焦点作一条渐近线的垂线，垂足恰好落在曲线
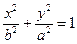上，则双曲线的离心率为________________.