题目内容
若集合M={x|x2+x-6=0},N={x|ax-1=0},且M∩N=N,则实数a的取值组成的集合是
- A.{
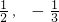 }
} - B.{
 ,
, }
} - C.{
 ,0,
,0, }
} - D.{-
 ,0,
,0, }
}
D
分析:先求出M,再通过讨论a的取值求出集合N,根据条件M∩N=N知集合N的元素也是集合M的元素,列方程求解即可
解答:由x2+x-6=0,得x=-3或x=2
∴M={-3,2}
又∵N={x|ax-1=0}
当a=0时,N=∅,满足M∩N=N
当a≠0时,解得x= ,即N={
,即N={ }
}
∵M∩N=N
∴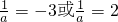
∴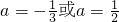
∴a组成的集合为{ ,0,
,0, }
}
故选D
点评:本题考查集合之间的关系,把集合与集合的关系转化为元素之间的关系.要知道M∩N=N等价于N⊆M,注意空集是任意集合的子集.属简单题
分析:先求出M,再通过讨论a的取值求出集合N,根据条件M∩N=N知集合N的元素也是集合M的元素,列方程求解即可
解答:由x2+x-6=0,得x=-3或x=2
∴M={-3,2}
又∵N={x|ax-1=0}
当a=0时,N=∅,满足M∩N=N
当a≠0时,解得x=
 ,即N={
,即N={ }
}∵M∩N=N
∴
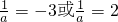
∴
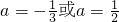
∴a组成的集合为{
 ,0,
,0, }
}故选D
点评:本题考查集合之间的关系,把集合与集合的关系转化为元素之间的关系.要知道M∩N=N等价于N⊆M,注意空集是任意集合的子集.属简单题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目