题目内容
讨论函数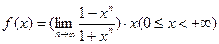 在
在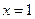 与
与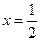 点处的连续性
点处的连续性
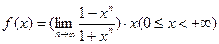 在
在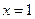 与
与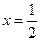 点处的连续性
点处的连续性(1)求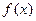 的表达式:
的表达式:
①当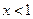 时,
时,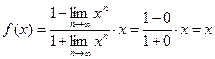
②当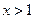 时,
时,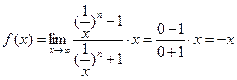
③当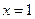 时,
时,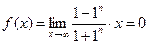
∴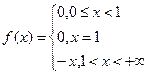
(2)讨论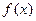 在
在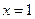 点处的连续性:
点处的连续性:
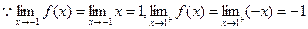
∴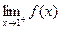 不存在,
不存在,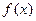 在
在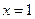 点处不连续
点处不连续
(3)讨论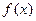 在
在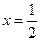 点处的连续性:
点处的连续性:
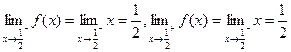
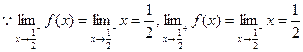
∴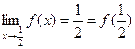 ,
,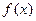 在
在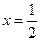 点处连续.
点处连续.
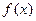 的表达式:
的表达式:①当
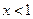 时,
时,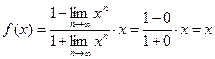
②当
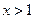 时,
时,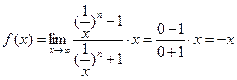
③当
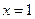 时,
时,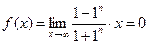
∴
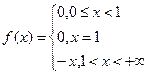
(2)讨论
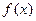 在
在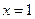 点处的连续性:
点处的连续性: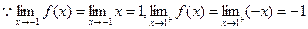
∴
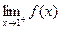 不存在,
不存在,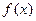 在
在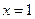 点处不连续
点处不连续(3)讨论
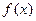 在
在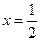 点处的连续性:
点处的连续性: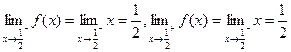
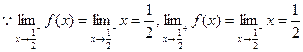
∴
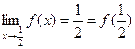 ,
,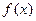 在
在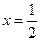 点处连续.
点处连续.分类讨论不仅是解决问题的一种逻辑方法,也是一种重要的数学思想.
明确讨论对象,确立分类标准,正确进行分类,以获得阶段性的结论,最后归纳综合得出结果,是分类讨论的实施方法.本题极限式中,若不能对x以1为标准,分三种情况分别讨论,则无法获得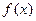 的表达式,使解答搁浅.
的表达式,使解答搁浅.
讨论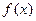 在
在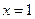 与
与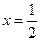 点处的连续性,若作出
点处的连续性,若作出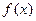 的图像,则可由图像的直观信息中得出结论,再据定义进行解析论证.
的图像,则可由图像的直观信息中得出结论,再据定义进行解析论证.
由于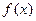 的表达式并非显式,所以须先求出
的表达式并非显式,所以须先求出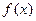 的解析式,再讨论其连续性,其中极限式中含
的解析式,再讨论其连续性,其中极限式中含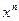 ,故须分类讨论.
,故须分类讨论.
明确讨论对象,确立分类标准,正确进行分类,以获得阶段性的结论,最后归纳综合得出结果,是分类讨论的实施方法.本题极限式中,若不能对x以1为标准,分三种情况分别讨论,则无法获得
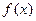 的表达式,使解答搁浅.
的表达式,使解答搁浅.讨论
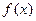 在
在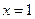 与
与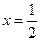 点处的连续性,若作出
点处的连续性,若作出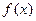 的图像,则可由图像的直观信息中得出结论,再据定义进行解析论证.
的图像,则可由图像的直观信息中得出结论,再据定义进行解析论证.由于
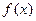 的表达式并非显式,所以须先求出
的表达式并非显式,所以须先求出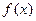 的解析式,再讨论其连续性,其中极限式中含
的解析式,再讨论其连续性,其中极限式中含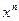 ,故须分类讨论.
,故须分类讨论.
练习册系列答案
相关题目
 在区间
在区间 上处处连续,则常数
上处处连续,则常数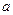 的值为( )
的值为( )


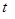 (s)时的速度为
(s)时的速度为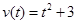 ,则
,则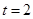 时物体的加速度为 .
时物体的加速度为 .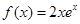 在
在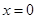 处的导数
处的导数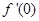 = .
= .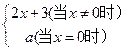 (当x
(当x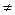 0时) ,点在x=0处连续,则
0时) ,点在x=0处连续,则 。
。 是连续函数,则
是连续函数,则 ( )
( )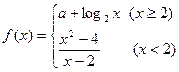 在点
在点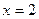 处连续,则常数
处连续,则常数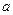 的值是
的值是 ,要使函数
,要使函数 在
在 内连续,则
内连续,则 的值为 .
的值为 . 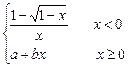 处处连续,则a的值为_________.
处处连续,则a的值为_________.