题目内容
(本题12分)如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=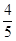 |PD|.
|PD|.
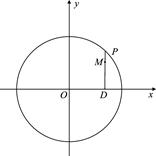
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为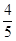 的直线被曲线C所截线段的长度.
的直线被曲线C所截线段的长度.
【答案】
(Ⅰ)设M(x,y),P(xp,yp),由已知得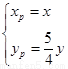
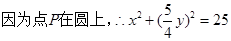 ,即C的方程为:
,即C的方程为: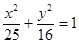 。……………………5分
。……………………5分
(Ⅱ) 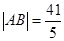
【解析】
试题分析:(Ⅰ)设M(x,y),P(xp,yp),由已知得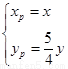
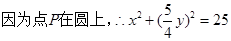 ,即C的方程为:
,即C的方程为: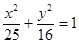 。……………………5分
。……………………5分
(Ⅱ) 过点(3,0)且斜率为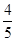 的直线l为
的直线l为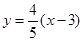
设直线l与C的交点为A(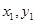 ), B(
), B(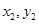 )
)
由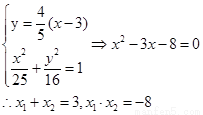
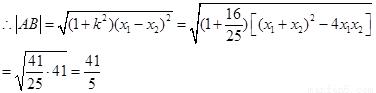
………………………………………………………………12分
考点:本题主要考查椭圆的标准方程,直线与椭圆的位置关系。
点评:容易题,涉及直线与圆锥曲线的位置关系问题,往往要利用韦达定理。弦长公式要清楚。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
 中,
中,  ,点
,点 是棱
是棱 上一点.
上一点.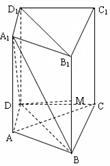
 面
面 ;
; ;
; 中,
中,  ,点
,点 是棱
是棱 上一点
上一点 面
面 ;
; ;
;
 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.