题目内容
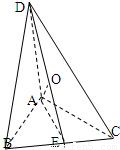
14、我们知道在平面几何中,(如图所示)若△ABC中,AB⊥AC,AD⊥BC,D是垂足,则AB2=BD•BC.类比可得,若三棱锥A-BCD中,AD⊥面ABC,AO⊥面BCD,O为垂足,则
S△BCO2=S△BCA•S△BCD
.
分析:这是一个类比推理的题,在由平面图形到空间图形的类比推理中,一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由已知在平面几何中,(如图所示)若△ABC中,AB⊥AC,AD⊥BC,D是垂足,则AB2=BD•BC,我们可以类比这一性质,推理出若三棱锥A-BCD中,AD⊥面ABC,AO⊥面BCD,O为垂足,则S△BCO2=S△BCA•S△BCD
解答:解:由已知在平面几何中,
若△ABC中,AB⊥AC,AD⊥BC,D是垂足,
则AB2=BD•BC,
我们可以类比这一性质,推理出:
若三棱锥A-BCD中,AD⊥面ABC,AO⊥面BCD,O为垂足,
则.S△BCO2=S△BCA•S△BCD
故答案为:S△BCO2=S△BCA•S△BCD
若△ABC中,AB⊥AC,AD⊥BC,D是垂足,
则AB2=BD•BC,
我们可以类比这一性质,推理出:
若三棱锥A-BCD中,AD⊥面ABC,AO⊥面BCD,O为垂足,
则.S△BCO2=S△BCA•S△BCD
故答案为:S△BCO2=S△BCA•S△BCD
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目