题目内容
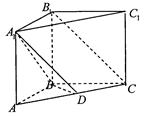
在直三棱柱ABC—A1B1C1中,AB=BC=BB1,D为AC的中点,
(1)求证:B1C∥平面A1BD; (2)若AC1⊥平面A1BD,二面角B—A1C1—D的余弦值.
|
(1)证明见解析 (2)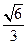
(1)连结AB1交于A1B于点E,连结ED.
∵侧面ABB1A1是正方形 ∴E是AB1的中点
又∵D是AC的中点 ∴ED∥B1C
∴B1C∥平面A1BD………………4分
(2)取A1C1的中点G,连结DG,则DG⊥A1C1
∵AB=BC ∴BD⊥AC ∴BD⊥平面A1C1D
∴BG⊥A1C1
∴∠BGD为二面角B—A1C1—D的平面角………………8分
∵AC1⊥平面A1BD,∴AC1⊥BD,又∵CC1⊥平面ABCD,且AC1在平面ABC的射影为AC,∴AC⊥BD
∵AB=BC且D为AC中点,∴AB⊥BC 且BD=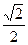 AB
AB
又∵DG=A1A=AB
∴BG=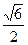 AB ∴
AB ∴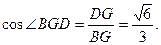 ……………………12分
……………………12分
∵侧面ABB1A1是正方形 ∴E是AB1的中点
又∵D是AC的中点 ∴ED∥B1C
∴B1C∥平面A1BD………………4分
(2)取A1C1的中点G,连结DG,则DG⊥A1C1
∵AB=BC ∴BD⊥AC ∴BD⊥平面A1C1D
∴BG⊥A1C1
∴∠BGD为二面角B—A1C1—D的平面角………………8分
∵AC1⊥平面A1BD,∴AC1⊥BD,又∵CC1⊥平面ABCD,且AC1在平面ABC的射影为AC,∴AC⊥BD
∵AB=BC且D为AC中点,∴AB⊥BC 且BD=
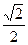 AB
AB又∵DG=A1A=AB
∴BG=
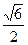 AB ∴
AB ∴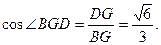 ……………………12分
……………………12分
练习册系列答案
相关题目
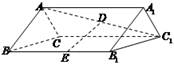
 的底面边长是2,D是侧棱
的底面边长是2,D是侧棱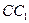 的中点,平面ABD和平面
的中点,平面ABD和平面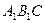 的交线为MN.
的交线为MN.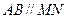 ;
;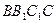 所成的角为
所成的角为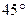 ,试求二面角
,试求二面角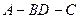 的大小.
的大小.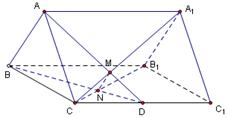
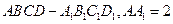 ,
, 为棱
为棱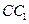 的中点.
的中点.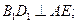
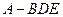 的体积;
的体积;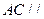 平面
平面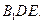 .
. 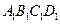 的棱长为l,点F为
的棱长为l,点F为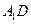 的中点.
的中点.
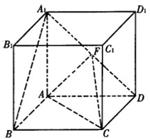
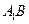 ∥平面AFC;.
∥平面AFC;.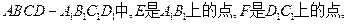
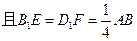 ,求
,求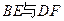 所成角的正弦值。
所成角的正弦值。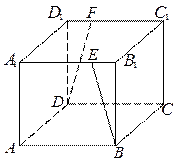
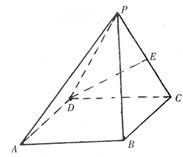
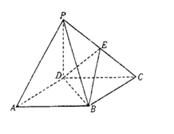
 为正方形
为正方形 所在平面外一点
所在平面外一点 平面
平面 分别是线段
分别是线段 的中点。w. (I)求证:
的中点。w. (I)求证: 平面
平面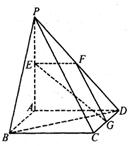
 平面
平面 ;
; 与
与 所成角的大小。
所成角的大小。