题目内容
甲、乙两位同学进行篮球三分球投篮比赛,甲每次投中的概率为 ,乙每次投中的概率为
,乙每次投中的概率为 ,每人分别进行三次投篮.
,每人分别进行三次投篮.
(Ⅰ)记甲投中的次数为ξ,求ξ的分布列及数学期望Eξ;
(Ⅱ)求乙至多投中2次的概率;
(Ⅲ)求乙恰好比甲多投进2次的概率.
解:(Ⅰ)ξ的可能取值为:0,1,2,3. …(1分)
则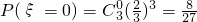 ;
;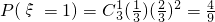 ;
;
 ;
;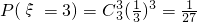 .
.
ξ的分布列如下表:
…(4分)
∴ . …(5分)
. …(5分)
(Ⅱ)利用对立事件,可得乙至多投中2次的概率为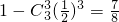 . …(8分)
. …(8分)
(Ⅲ)设乙比甲多投中2次为事件A,乙恰投中2次且甲恰投中0次为事件B1,乙恰投中3次且甲恰投中1次为事件B2,
则A=B1∪B2,B1,B2为互斥事件. …(10分)
所以P(A)=P(B1)+P(B2)=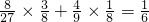 .
.
所以乙恰好比甲多投中2次的概率为 . …(13分)
. …(13分)
分析:(Ⅰ)确定ξ的可能取值,求出相应的概率,即可得到ξ的分布列及数学期望Eξ;
(Ⅱ)利用对立事件,可得乙至多投中2次的概率;
(Ⅲ)设乙比甲多投中2次为事件A,乙恰投中2次且甲恰投中0次为事件B1,乙恰投中3次且甲恰投中1次为事件B2,
则A=B1∪B2,利用互斥事件的概率公式,即可求得结论.
点评:本题考查离散型随机变量的分布列与数学期望,解题的关键是确定变量的取值,求出相应的概率.
则
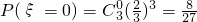 ;
;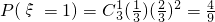 ;
; ;
;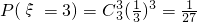 .
.ξ的分布列如下表:
| ξ | 0 | 1 | 2 | 3 |
| P |  |  |  |  |
∴
 . …(5分)
. …(5分)(Ⅱ)利用对立事件,可得乙至多投中2次的概率为
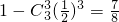 . …(8分)
. …(8分)(Ⅲ)设乙比甲多投中2次为事件A,乙恰投中2次且甲恰投中0次为事件B1,乙恰投中3次且甲恰投中1次为事件B2,
则A=B1∪B2,B1,B2为互斥事件. …(10分)
所以P(A)=P(B1)+P(B2)=
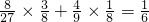 .
.所以乙恰好比甲多投中2次的概率为
 . …(13分)
. …(13分)分析:(Ⅰ)确定ξ的可能取值,求出相应的概率,即可得到ξ的分布列及数学期望Eξ;
(Ⅱ)利用对立事件,可得乙至多投中2次的概率;
(Ⅲ)设乙比甲多投中2次为事件A,乙恰投中2次且甲恰投中0次为事件B1,乙恰投中3次且甲恰投中1次为事件B2,
则A=B1∪B2,利用互斥事件的概率公式,即可求得结论.
点评:本题考查离散型随机变量的分布列与数学期望,解题的关键是确定变量的取值,求出相应的概率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,乙每次投中的概率为
,乙每次投中的概率为 ,每人分别进行三次投篮.
,每人分别进行三次投篮.