题目内容
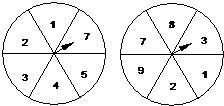 如图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均等,那么两个指针同时落在奇数所在区域的概率是
如图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均等,那么两个指针同时落在奇数所在区域的概率是分析:由题意知本题是一个相互独立事件同时发生的概率,指针在本圆盘每个数所在区域的机会均等,可以用几何概型公式求出概率,
对于第一个圆盘和第二个圆盘来说指针落在奇数区域的概率一样,根据相互独立事件同时发生的概率得到结果.
对于第一个圆盘和第二个圆盘来说指针落在奇数区域的概率一样,根据相互独立事件同时发生的概率得到结果.
解答:解:根据题意,可得指针在本圆盘每个数所在区域的机会均等,
∴对于第一个圆盘来说指针落在奇数区域的概率是
=
,
对于第二个圆盘来说指针落在奇数区域的概率是
=
,
∴两个指针同时落在奇数所在区域的概率是
×
=
,
故答案为:
.
∴对于第一个圆盘来说指针落在奇数区域的概率是
| 4 |
| 6 |
| 2 |
| 3 |
对于第二个圆盘来说指针落在奇数区域的概率是
| 4 |
| 6 |
| 2 |
| 3 |
∴两个指针同时落在奇数所在区域的概率是
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
故答案为:
| 4 |
| 9 |
点评:本题是一个相互独立事件同时发生的概率和几何概型,几何概型和古典概型是高中必修中学习的高考时常以选择和填空出现,有时文科会考这种类型的解答.

练习册系列答案
相关题目
如图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均等,那么两个指针同时落在奇数所在区域的概率是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
 的事件的概率是
的事件的概率是
 B.
B. C.
C. D.
D.
 B.
B.

 D.
D.

 (B).
(B). (C).
(C). (D).
(D).
