题目内容
 已知椭圆:
已知椭圆: .
.
(Ⅰ)若椭圆的一个焦点到长轴的两个端点的距离分别为 和
和 ,求椭圆的方程;
,求椭圆的方程;
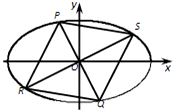
(Ⅱ)如图,过坐标原点O任作两条互相垂直的直线与椭圆分别交于P、Q和R、S四点.设原点O到四边形PRQS某一边的距离为d,试求:当d=1时 的值.
的值.
解:(Ⅰ)∵椭圆的一个焦点到长轴的两个端点的距离分别为 和
和 ,
,
∴2a=4,a=2,2c=2 ,c=
,c= ,
,
∴椭圆的方程:
(Ⅱ)由椭圆的对称性知:PRQS为菱形,原点O到各边距离相等
(1)当P在y轴上时,易知R在x轴上,此时PR方程为 ,d=1?
,d=1?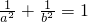 .
.
(2)当P在x轴上时,易知R在y轴上,此时PR方程为 ,d=1?
,d=1?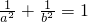 .
.
(3)当P不在坐标轴上时,设PQ斜率为k,P(x1,kx1)、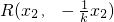
P在椭圆上,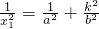 ①;
①;
R在椭圆上,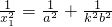 ②
②
利用Rt△POR可得 d|PR|=|OP|•|OR|
即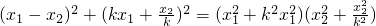
整理得 .再将①②代入,得
.再将①②代入,得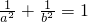
综上当d=1时,有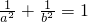 .
.
分析:(Ⅰ)由椭圆的一个焦点到长轴的两个端点的距离分别为 和
和 ,知2a=4,2c=2
,知2a=4,2c=2 ,由此能求出椭圆的方程.
,由此能求出椭圆的方程.
(Ⅱ)由椭圆的对称性知:PRQS为菱形,原点O到各边距离相等.当P在y轴上时,R在x轴上,PR方程为 ,
,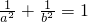 .当P在x轴上时,R在y轴上,PR方程为
.当P在x轴上时,R在y轴上,PR方程为 ,
,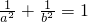 .当P不在坐标轴上时,设PQ斜率为k,P(x1,kx1)、
.当P不在坐标轴上时,设PQ斜率为k,P(x1,kx1)、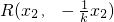 ,P在椭圆上,
,P在椭圆上,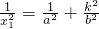 ,R在椭圆上,
,R在椭圆上,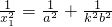 .利用Rt△POR得d|PR|=|OP|•|OR|,由此得
.利用Rt△POR得d|PR|=|OP|•|OR|,由此得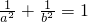 .故当d=1时,有
.故当d=1时,有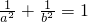 .
.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意分类讨论思想的合理运用.
 和
和 ,
,∴2a=4,a=2,2c=2
 ,c=
,c= ,
,∴椭圆的方程:

(Ⅱ)由椭圆的对称性知:PRQS为菱形,原点O到各边距离相等
(1)当P在y轴上时,易知R在x轴上,此时PR方程为
 ,d=1?
,d=1?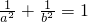 .
.(2)当P在x轴上时,易知R在y轴上,此时PR方程为
 ,d=1?
,d=1?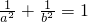 .
.(3)当P不在坐标轴上时,设PQ斜率为k,P(x1,kx1)、
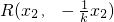
P在椭圆上,
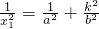 ①;
①;R在椭圆上,
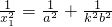 ②
②利用Rt△POR可得 d|PR|=|OP|•|OR|
即
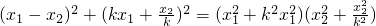
整理得
 .再将①②代入,得
.再将①②代入,得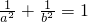
综上当d=1时,有
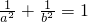 .
.分析:(Ⅰ)由椭圆的一个焦点到长轴的两个端点的距离分别为
 和
和 ,知2a=4,2c=2
,知2a=4,2c=2 ,由此能求出椭圆的方程.
,由此能求出椭圆的方程.(Ⅱ)由椭圆的对称性知:PRQS为菱形,原点O到各边距离相等.当P在y轴上时,R在x轴上,PR方程为
 ,
,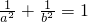 .当P在x轴上时,R在y轴上,PR方程为
.当P在x轴上时,R在y轴上,PR方程为 ,
,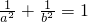 .当P不在坐标轴上时,设PQ斜率为k,P(x1,kx1)、
.当P不在坐标轴上时,设PQ斜率为k,P(x1,kx1)、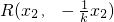 ,P在椭圆上,
,P在椭圆上,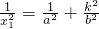 ,R在椭圆上,
,R在椭圆上,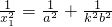 .利用Rt△POR得d|PR|=|OP|•|OR|,由此得
.利用Rt△POR得d|PR|=|OP|•|OR|,由此得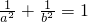 .故当d=1时,有
.故当d=1时,有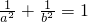 .
.点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意分类讨论思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 :
:
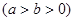 ,
, ,求椭圆的标准方程;
,求椭圆的标准方程; 的直线
的直线 与椭圆
与椭圆 ,且
,且 为锐角(
为锐角( 为坐标原点),求直线
为坐标原点),求直线 的取值范围;
的取值范围; 四点,设原点
四点,设原点 的一边距离为
的一边距离为 ,试求
,试求 时
时 满足的条件.
满足的条件.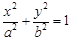 (
(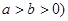 .
.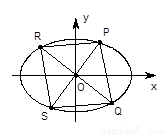
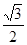 ,求椭圆的标准方程;
,求椭圆的标准方程;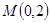 的直线
的直线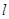 与椭圆C交于不同的两点
与椭圆C交于不同的两点 ,且
,且 为锐角(其中
为锐角(其中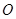 为坐标原点),求直线
为坐标原点),求直线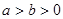 )相交于
)相交于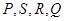 四点,设原点
四点,设原点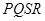 一边的距离为
一边的距离为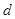 ,试求
,试求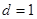 时
时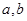 满足的条件.
满足的条件. ,若椭圆的焦距为
,若椭圆的焦距为 ,则
,则 的取值集合为
。
的取值集合为
。 :
: 的左焦点
的左焦点 ,若椭圆上存在一点
,若椭圆上存在一点 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段 相切于线段
相切于线段 .
. 及椭圆
及椭圆 :
: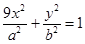 ,过点
,过点 作斜率为
作斜率为 的直线
的直线 交椭圆
交椭圆 两点,设线段
两点,设线段 的中点为
的中点为 ,连结
,连结 ,试问当
,试问当 的直线交椭圆
的直线交椭圆 :
: 于
于 、
、 两点,其中
两点,其中 轴的垂线,垂足为
轴的垂线,垂足为 ,连结
,连结 并延长交椭圆
并延长交椭圆 ,求证:
,求证:
 ,若椭圆上存在点
,若椭圆上存在点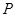 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段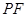 相切于线段
相切于线段 为
为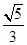 B.
B. C.
C. D.
D.