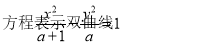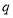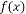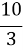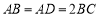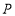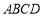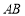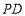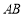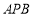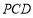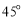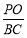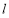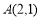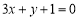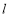题目内容
已知椭圆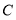
：
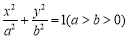的短轴长为2，离心率为
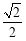，设过右焦点的直线
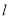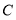与椭圆交于不同的两点A，B，过A，B作直线
的垂线AP，BQ，垂足分别为P，Q．记
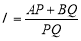， 若直线l的斜率
≥
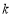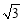,则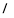
的取值范围为 ．
.
【解析】
试题分析：根据已知条件求出椭圆C的方程，再由直线l过椭圆C的右焦点，设出直线l的方程，联系椭圆C和直线l的方程组，利用一元二次方程根与系数的关系能求出λ的取值范围．
考点：(1)直线与圆锥曲线的综合问题；(2)椭圆的应用．
练习册系列答案
相关题目
