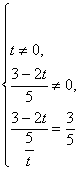Question

设数列{A_n}的首项A₁=t,前n项和为S_n,满足：

   5S_n－3S_n－1=3(n≥2，n∈N).

是否存在常数t，使得数列{A_n}为等比数列，若存在，求出t的值，若不存在请说明理由.

Answer 1

答案：
解析：

由己知5Sn－3Sn－1=3(n≥2，n∈N).　　   ① 得5Sn+1－3Sn=3.　　　　　　　　　　　　  ② ②－①，得5An+1－3An=0(n≥2，n∈N), 即5An+1=3An(n≥2，n∈N). 故n≥2，n∈N时，=. 又∵5S2－3S1=3， ∴5（A2+t）－3t=3，故A2=. ∴{An}为等比数列的充要条件为  解得t=.   ∴t=时，{An}是以A1=,公比q=的等比数列.