题目内容
如图,在直四棱柱 中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, "
中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, "  ="2, " E、
="2, " E、 分别是棱AD、A
分别是棱AD、A 的中点.
的中点. 


(1) 设F是棱AB的中点,证明:直线E //平面FC
//平面FC ;
;
(2 ) 证明:平面D1AC⊥平面BB1C1C.
) 证明:平面D1AC⊥平面BB1C1C.
 中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, "
中,底面ABCD为等腰梯形,AB//CD,AB="4," BC="CD=2, "  ="2, " E、
="2, " E、 分别是棱AD、A
分别是棱AD、A 的中点.
的中点. 


(1) 设F是棱AB的中点,证明:直线E
 //平面FC
//平面FC ;
;(2
 ) 证明:平面D1AC⊥平面BB1C1C.
) 证明:平面D1AC⊥平面BB1C1C.19.证明:(1)在直四棱柱ABCD-A
 B
B C
C D
D 中,取A1B1的中点F1,
中,取A1B1的中点F1,连接A1D,C1F1,CF
 1,因为AB="4," CD=2,且AB//CD,
1,因为AB="4," CD=2,且AB//CD,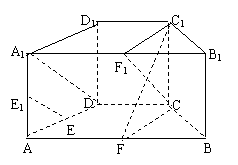
所以CDA1F1,A1F1CD为平行四边形,所以CF1//A1D,
又因为E、E
 分别是棱AD、AA
分别是棱AD、AA 的中点,所以EE1//A1D,
的中点,所以EE1//A1D,所以CF1//EE1,又因为
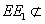 平面FCC
平面FCC ,
,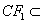 平面FCC
平面FCC ,所以直线EE
,所以直线EE //平面FCC
//平面FCC .
.(2)连接AC,在直棱柱中,
 CC1⊥平面ABCD,AC
CC1⊥平面ABCD,AC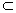 平面ABCD,
平面ABCD,所以CC1⊥AC,因为底面ABCD为等腰梯形,AB="4," BC=2,
F是棱AB的中点,所以CF=CB=BF,△BCF为正三角形,
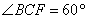 ,△ACF为等腰三角形,且
,△ACF为等腰三角形,且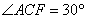
所以AC⊥BC, 又因为BC与CC1都在平面BB1C1C内且交于点C, 所以AC⊥平面BB1C1C,而
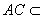 平面D1AC,所以平面D1AC⊥平面BB1C1C.
平面D1AC,所以平面D1AC⊥平面BB1C1C.略

练习册系列答案
相关题目
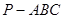 中,
中,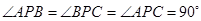 ,
,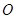 在
在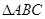 内,
内,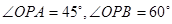 ,则
,则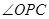 的度数为( )
的度数为( )



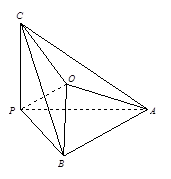
 ,则P到这三个平面的距离分别是( )
,则P到这三个平面的距离分别是( )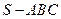 中,各个侧面都是边长为
中,各个侧面都是边长为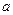 的正三角形,
的正三角形,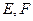 分别是
分别是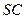 和
和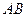 的中点,则异面直线
的中点,则异面直线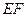 与
与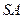 所成的角等于( )
所成的角等于( )




 在平面
在平面 外,
外, ,
, ,
, 、
、 分别是
分别是 和
和 的中点,则
的中点,则 的长是( )
的长是( )



 中,
中, 是
是 的中点,
的中点, 是底面
是底面 的中心,
的中心, 是
是 上的任意点,则直线与所成的角为
上的任意点,则直线与所成的角为