题目内容
下列命题:
①设a,b是非零实数,若a<b,则ab2<a2b;
②若a<b<0,则
>
;
③函数y=
的最小值是2;
④若x、y是正数,且
+
=1,则xy有最小值16.
其中正确命题的序号是
①设a,b是非零实数,若a<b,则ab2<a2b;
②若a<b<0,则
| 1 |
| a |
| 1 |
| b |
③函数y=
| x2+3 | ||
|
④若x、y是正数,且
| 1 |
| x |
| 4 |
| y |
其中正确命题的序号是
②④
②④
.分析:①的结论不成立,举出反例即可;
②由同号不等式取倒数法则,知,知②成立;
③函数y=
=
+
≥2的前提条件是
=1,由
≥2,知函数y=
的最小值不是2;
④由x、y是正数,且
+
=1,知
≤(
)2=
,故xy≥16.
②由同号不等式取倒数法则,知,知②成立;
③函数y=
| x2+3 | ||
|
| x2+2 |
| 1 | ||
|
| x2+2 |
| x2+2 |
| x2+3 | ||
|
④由x、y是正数,且
| 1 |
| x |
| 4 |
| y |
| 4 |
| xy |
| 1 |
| 2 |
| 1 |
| 4 |
解答:解:设a,b是非零实数,若a<b,则ab2<a2b,此结论不成立,
反例:令a=-10,b=-1,则ab2=-10>a2b=-100,故①不成立;
若a<b<0,由同号不等式取倒数法则,知
>
,故②成立;
函数y=
=
+
≥2的前提条件是
=1,
∵
≥2,∴函数y=
的最小值不是2,故③不正确;
∵x、y是正数,且
+
=1,
∴
≤(
)2=
,
∴xy≥16,故④正确.
故答案为:②④.
反例:令a=-10,b=-1,则ab2=-10>a2b=-100,故①不成立;
若a<b<0,由同号不等式取倒数法则,知
| 1 |
| a |
| 1 |
| b |
函数y=
| x2+3 | ||
|
| x2+2 |
| 1 | ||
|
| x2+2 |
∵
| x2+2 |
| x2+3 | ||
|
∵x、y是正数,且
| 1 |
| x |
| 4 |
| y |
∴
| 4 |
| xy |
| 1 |
| 2 |
| 1 |
| 4 |
∴xy≥16,故④正确.
故答案为:②④.
点评:本题考查命题的真假判断,解题时要注意同号不等式取倒数法则、均值不等式成立的条件等知识点的灵活运用.

练习册系列答案
相关题目
 ,
, ;
; 是周期为2
是周期为2 的偶函数;
的偶函数; 的焦点为F,点P为抛物线上任意一点,则
的焦点为F,点P为抛物线上任意一点,则 的最小值为2;
的最小值为2; +x-2=0”的否命题为“若x=1,则
+x-2=0”的否命题为“若x=1,则 x0∈(-∞,0],
x0∈(-∞,0], ≥1,则
≥1,则 p:
p: x∈(0,+∞),
x∈(0,+∞), <1;
<1;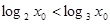 ,命题q:
,命题q: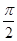 ),tanx>sinx
),tanx>sinx <1”的必要不充分条件.
<1”的必要不充分条件.