题目内容
在△ABC中,a2+b2=c2+ab,且cosAcosB=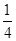 ,试判断△ABC的形状。
,试判断△ABC的形状。
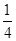 ,试判断△ABC的形状。
,试判断△ABC的形状。等边三角形
由a2+b2=c2+ab,知,用余弦定理可求出C角,
解:由余弦定理,得c2=a2+b2-2abcosC.
∵a2+b2=c2+ab,∴ab-2abcosC=0.
∴cosC=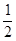 ,∴C=60°
,∴C=60°
∵cosAcosB=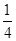 ,cos(A+B)=cos(180°-C)=cos120°=-
,cos(A+B)=cos(180°-C)=cos120°=-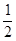 ,
,
cos(A+B)=cosAcosB-sinAsinB,∴sinAsinB=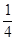 .
.
∴cos(A-B)=cosAcosB+sinAsinB=1.
∵-π<A-B<π,∴A-B=0.
∴A=B=60°
解:由余弦定理,得c2=a2+b2-2abcosC.
∵a2+b2=c2+ab,∴ab-2abcosC=0.
∴cosC=
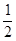 ,∴C=60°
,∴C=60°∵cosAcosB=
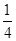 ,cos(A+B)=cos(180°-C)=cos120°=-
,cos(A+B)=cos(180°-C)=cos120°=-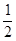 ,
,cos(A+B)=cosAcosB-sinAsinB,∴sinAsinB=
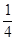 .
.∴cos(A-B)=cosAcosB+sinAsinB=1.
∵-π<A-B<π,∴A-B=0.
∴A=B=60°

练习册系列答案
相关题目
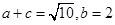 ,求△ABC的面积.
,求△ABC的面积. 为锐角,
为锐角, ,求
,求 的值.
的值.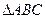 中,A、B、C为它的三个内角,设向量
中,A、B、C为它的三个内角,设向量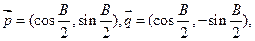 且
且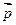 与
与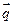 的夹角为
的夹角为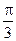 .(Ⅰ)求角
.(Ⅰ)求角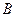 的大小; (Ⅱ) 已知
的大小; (Ⅱ) 已知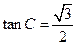 ,求
,求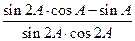 的值.
的值.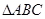 中,角
中,角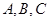 所对的边分别为
所对的边分别为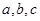 ,若
,若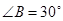 ,
,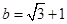 ,则
,则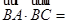 .
. 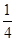 (b2+c2-a2),则A=( )
(b2+c2-a2),则A=( )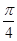
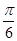
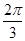
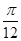
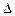 ABC中,已知
ABC中,已知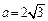 ,
,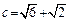 ,
,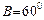 ,则A= 。
,则A= 。