题目内容
已知平面向量![]() =(
=(![]() –1),
–1), ![]() =(
=(![]() ).
).
(1)证明![]() ⊥
⊥![]() ;
;
(2)若存在不同时为零的实数k和t,使![]() =
=![]() +(t2–3)
+(t2–3) ![]() ,
,![]() =–k
=–k![]() +t
+t![]() ,且
,且![]() ⊥
⊥![]() ,试求函数关系式k=f(t);
,试求函数关系式k=f(t);
(3)据(2)的结论,讨论关于t的方程f(t)–k=0的解的情况.
(1)证明略,(2)k=![]() t(t2–3),(3)当k>
t(t2–3),(3)当k>![]() 或k<–
或k<–![]() 时,直线y=k与曲线y=f(t)仅有一个交点,则方程有一解;
时,直线y=k与曲线y=f(t)仅有一个交点,则方程有一解;
当k=![]() 或k=–
或k=–![]() 时,直线与曲线有两个交点,则方程有两解;当k=0,直线与曲线有三个交点,但k、t不同时为零,故此时也有两解;当–
时,直线与曲线有两个交点,则方程有两解;当k=0,直线与曲线有三个交点,但k、t不同时为零,故此时也有两解;当–![]() <k<0或0<k<
<k<0或0<k<![]() 时,直线与曲线有三个交点,则方程有三个解.
时,直线与曲线有三个交点,则方程有三个解.
解析:
(1)证明: ∵![]() ·
·![]() =
=![]() =0,∴
=0,∴![]() ⊥
⊥![]()
(2)解: ∵![]() ⊥
⊥![]() ,∴
,∴![]() ·
·![]() =
=![]()
即[![]() +(t2–3)
+(t2–3) ![]() ]·(–k
]·(–k![]() +t
+t![]() )=0,整理后得
)=0,整理后得
–k![]() 2+[t–k(t2–3)]
2+[t–k(t2–3)]![]() ·
·![]() +t(t2–3)·
+t(t2–3)·![]() 2=0
2=0
∵![]() ·
·![]() =0,
=0, ![]() 2=4,
2=4, ![]() 2=1
2=1
∴上式化为–4k+t(t2–3)=0,∴k=![]() t(t2–3).
t(t2–3).
(3)解: 讨论方程![]() t(t2–3)–k=0的解的情况,
t(t2–3)–k=0的解的情况,
可以看作曲线f(t)=![]() t(t2–3)与直线y=k的交点个数
t(t2–3)与直线y=k的交点个数
于是f′(t)=![]() (t2–1)=
(t2–1)=![]() (t+1)(t–1).
(t+1)(t–1).
令f′(t)=0,解得t1=–1,t2=1![]() 当t变化时,f′(t),f(t)的变化情况如下表
当t变化时,f′(t),f(t)的变化情况如下表![]()
| t | (–∞,–1) | –1 | (–1,1) | 1 | (1,+∞) |
| f′(t) | + | 0 | – | 0 | + |
| f(t) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
当t=–1时,f(t)有极大值,f(t)极大值=![]() ;
;
当t=1时,f(t)有极小值,f(t)极小值=–![]() .
.
而f(t)=![]() (t2–3)t=0时,得t=–
(t2–3)t=0时,得t=–![]() ,0,
,0,![]() .
.
所以f(t)的图象大致如右:

于是当k>![]() 或k<–
或k<–![]() 时,直线y=k与曲线y=f(t)仅有一个交点,则方程有一解;
时,直线y=k与曲线y=f(t)仅有一个交点,则方程有一解;

练习册系列答案
相关题目
 =(
=( ,1),
,1), =(
=( ),
), ,
, ,
, .
.
 时,求
时,求 的取值范围;
的取值范围;  ,是否存在实数
,是否存在实数 ,使得
,使得 有最大值2,若存在,求出所有满足条件的
有最大值2,若存在,求出所有满足条件的 =(
=( ,1),
,1), =(
=( ),
), ,
,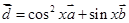 ,
, .(1)当
.(1)当 时,求
时,求 的取值范围;
的取值范围;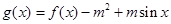 ,是否存在实数
,是否存在实数 ,使得
,使得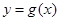 有最大值
有最大值 ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的