题目内容
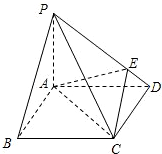 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=| 2 |
(1)求证:PA⊥平面ABCD.
(2)求二面角D-AC-E的正切值.
(3)在侧棱PC上是否存在一点F,使得BF∥平面AEC,若存在,指出F点位置,并证明,若不存在,说明理由.
分析:(1)由题意及图形利用线面垂直的判定定理即可得证;
(2)由于PA⊥平面ABCD,点E在PD线上,所过E作EG∥PA交AD于G,从而EG⊥平面ABCD,再利用三垂线定理或即可作出二面角的平面角;
(3)因为PA,AB,AD两两垂直,所以可以建立空间直角坐标系,假设PC存在一点,F使得BF∥平面AEC,利用方程的思想求解即可.
(2)由于PA⊥平面ABCD,点E在PD线上,所过E作EG∥PA交AD于G,从而EG⊥平面ABCD,再利用三垂线定理或即可作出二面角的平面角;
(3)因为PA,AB,AD两两垂直,所以可以建立空间直角坐标系,假设PC存在一点,F使得BF∥平面AEC,利用方程的思想求解即可.
解答: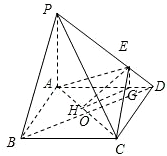 (1)证明:∵PA=AD=1,PD=
(1)证明:∵PA=AD=1,PD=
∴PA2+AD2=PD2即PA⊥AD
又∵PA⊥CD.AD∩CD=D
∴PA⊥平面ABCD
(2)解:过E作EG∥PA交AD于G,从而EG⊥平面ABCD′且AG=2GD.EG=
,PA=
.连接BD交AC于O,过G作GH∥OD交AC于H.
连接EH.∵GH⊥AC∴EH⊥AC
∴∠EHG为二面角D-AC-E的平面角.
∵HG=
OD=
.
∴tan∠EHG=
=
.
(3)解:因为PA,AB,AD两两垂直,所以A为原点,AB,AD,AP所在直线分别为x轴,y轴,Z轴建立空间直角坐标系.
则A(0,0,0)B(1,0,0)C(1,1,0)P(0,0,1)E(0,
,
)
=(1,1,0)
=(0,
)
设平面AEC的法向量
=(x,y,z),则
=
即
令y=1,则
=(-1,1,-2)
假设PC存在一点F且
=λ
(0≤λ≤1),使得BF∥平面AEC则
•
=0.
又∵
=
+
=(0,1,0)+(-λ,-λ,λ)=(-λ,1-λ,λ)
∴
•
=λ+1-λ-2λ=0∴λ=
∴存在P的中点F,使得BF∥平面AEC.
 (1)证明:∵PA=AD=1,PD=
(1)证明:∵PA=AD=1,PD=| 2 |
∴PA2+AD2=PD2即PA⊥AD
又∵PA⊥CD.AD∩CD=D
∴PA⊥平面ABCD
(2)解:过E作EG∥PA交AD于G,从而EG⊥平面ABCD′且AG=2GD.EG=
| 1 |
| 3 |
| 1 |
| 3 |
连接EH.∵GH⊥AC∴EH⊥AC
∴∠EHG为二面角D-AC-E的平面角.
∵HG=
| 2 |
| 3 |
| ||
| 3 |
∴tan∠EHG=
| EG |
| GH |
| ||
| 2 |
(3)解:因为PA,AB,AD两两垂直,所以A为原点,AB,AD,AP所在直线分别为x轴,y轴,Z轴建立空间直角坐标系.
则A(0,0,0)B(1,0,0)C(1,1,0)P(0,0,1)E(0,
| 2 |
| 3 |
| 1 |
| 3 |
| AC |
| AE |
| 2 |
| 3 |
| 1 |
| 3 |
设平面AEC的法向量
| n |
| n |
|
|
| n |
假设PC存在一点F且
| CF |
| CP |
| BF |
| n |
又∵
| BF |
| BC |
| CF |
∴
| BF |
| n |
| 1 |
| 2 |
∴存在P的中点F,使得BF∥平面AEC.
点评:(1)此问重点考查了利用计算证明线线垂直,还考查了线面垂直的判定定理的准确使用;
(2)此问重点考查了利用三垂线定理求其二面角的平面角,并考查了求角的大小放到三角形中进行求解;
(3)此问重点考查了利用空间向量的方法及假设存在于方程的思想进行求解的方法.
(2)此问重点考查了利用三垂线定理求其二面角的平面角,并考查了求角的大小放到三角形中进行求解;
(3)此问重点考查了利用空间向量的方法及假设存在于方程的思想进行求解的方法.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=