题目内容
已知函数 的图象在点(1,f(1))处得切线在y轴上的截距为3,若f(x)>x在(1,+∞)上恒成立,则a的取值范围是 .
的图象在点(1,f(1))处得切线在y轴上的截距为3,若f(x)>x在(1,+∞)上恒成立,则a的取值范围是 .
【答案】分析:先根据图象在点(1,f(1))处得切线在y轴上的截距为3,求得b=3-2a,再将f(x)>x在(1,+∞)上恒成立,转化为f(x)-x>0在(1,+∞)上恒成立,构造新函数,再进行分类讨论,即可确定a的取值范围.
解答:解:由题意,f(1)=2a+b∵函数
∴f′(x)=a-
∴f′(1)=0;
所以图象在点(1,f(1))处的切线为:y=f(1)=2a+b=3∴b=3-2a 若f(x)>x在(1,+∞)上恒成立即:f(x)-x>0在(1,+∞)上恒成立;
设g(x)=f(x)-x=(a-1)x+ +3-2a,
+3-2a,
∴g′(x)=a-1- a≤0时,x2>1,0<
a≤0时,x2>1,0< <1,∴0<
<1,∴0< <-a,∴a-1-
<-a,∴a-1-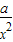 <-1<0; 0<a<1时,a-1<0,∴
<-1<0; 0<a<1时,a-1<0,∴ <0,∴a-1-
<0,∴a-1- <0;所以a<1时,g′(x)<0,g(x)在(1,+∞)上是减函数,
<0;所以a<1时,g′(x)<0,g(x)在(1,+∞)上是减函数,
∴g(x)>0不会恒成立,不满足题意;
把a=1代入可得:g(x)= +1>0在(1,+∞) 上恒成立,符合条件; a>1时,g′(x)=0 得:x=
+1>0在(1,+∞) 上恒成立,符合条件; a>1时,g′(x)=0 得:x= ;当x>
;当x>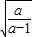 时,g′(x)>0;1<x<
时,g′(x)>0;1<x< 时,g′(x)<0 所以g(x)min=g
时,g′(x)<0 所以g(x)min=g )>0即可即:(a-1)
)>0即可即:(a-1) +
+ +3-2a>0
+3-2a>0
∴ ①当1<a≤
①当1<a≤ 时,上式恒成立; ②当a>
时,上式恒成立; ②当a> 时,平方得:4a2-4a>4a2-12a+9 即:a>
时,平方得:4a2-4a>4a2-12a+9 即:a> ;
;
∴a> 时,符合题意;综上可知:a的取值范围是:[1,+∞),
时,符合题意;综上可知:a的取值范围是:[1,+∞),
故答案为:[1,+∞)
点评:本题重点考查导数知识的运用,考查恒成立问题,解题时正确分类,利用导数确定函数的单调性是关键
解答:解:由题意,f(1)=2a+b∵函数

∴f′(x)=a-

∴f′(1)=0;
所以图象在点(1,f(1))处的切线为:y=f(1)=2a+b=3∴b=3-2a 若f(x)>x在(1,+∞)上恒成立即:f(x)-x>0在(1,+∞)上恒成立;
设g(x)=f(x)-x=(a-1)x+
 +3-2a,
+3-2a,∴g′(x)=a-1-
 a≤0时,x2>1,0<
a≤0时,x2>1,0< <1,∴0<
<1,∴0< <-a,∴a-1-
<-a,∴a-1-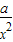 <-1<0; 0<a<1时,a-1<0,∴
<-1<0; 0<a<1时,a-1<0,∴ <0,∴a-1-
<0,∴a-1- <0;所以a<1时,g′(x)<0,g(x)在(1,+∞)上是减函数,
<0;所以a<1时,g′(x)<0,g(x)在(1,+∞)上是减函数,∴g(x)>0不会恒成立,不满足题意;
把a=1代入可得:g(x)=
 +1>0在(1,+∞) 上恒成立,符合条件; a>1时,g′(x)=0 得:x=
+1>0在(1,+∞) 上恒成立,符合条件; a>1时,g′(x)=0 得:x= ;当x>
;当x>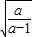 时,g′(x)>0;1<x<
时,g′(x)>0;1<x< 时,g′(x)<0 所以g(x)min=g
时,g′(x)<0 所以g(x)min=g )>0即可即:(a-1)
)>0即可即:(a-1) +
+ +3-2a>0
+3-2a>0∴
 ①当1<a≤
①当1<a≤ 时,上式恒成立; ②当a>
时,上式恒成立; ②当a> 时,平方得:4a2-4a>4a2-12a+9 即:a>
时,平方得:4a2-4a>4a2-12a+9 即:a> ;
; ∴a>
 时,符合题意;综上可知:a的取值范围是:[1,+∞),
时,符合题意;综上可知:a的取值范围是:[1,+∞),故答案为:[1,+∞)
点评:本题重点考查导数知识的运用,考查恒成立问题,解题时正确分类,利用导数确定函数的单调性是关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象在点
的图象在点 处的切线方程是
处的切线方程是 ,则
,则 .
. 的图象在点
的图象在点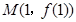 处的切线方程是
处的切线方程是 ,则
,则 ____.
____.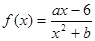 的图象在点M(-1,f(-1))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(-1))处的切线方程为x+2y+5=0. 的图象在点
的图象在点 处的切线的斜率为
处的切线的斜率为 ,且在
,且在 处取得极小值。
处取得极小值。 的解析式;
的解析式;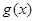 定义域为实数集
定义域为实数集 ,若存在区间
,若存在区间 ,使得
,使得 的值域也是
的值域也是 时,请写出函数
时,请写出函数 的一个“保值区间”(不必证明);
的一个“保值区间”(不必证明); 时,问
时,问 的图象在点
的图象在点 处的切线的方程为
处的切线的方程为 。
。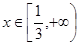 有
有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 在区间
在区间 内有零点,求实数
内有零点,求实数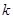 的最大值。
的最大值。