题目内容
已知函数 (x∈R)的最大值为M,最小值为m,则M+m= .
(x∈R)的最大值为M,最小值为m,则M+m= .
【答案】分析:先把函数 变形为
变形为 ,令
,令 ,,可判断函数g(x)的奇偶性,据此找到
,,可判断函数g(x)的奇偶性,据此找到
g(x)的最大值与最小值之间的关系,在有f(x)=1+g(x),求出f(x)的最大值与最小值之和.
解答:解:函数 可变形为
可变形为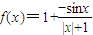
令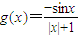 ,,则
,,则 =-g(x),
=-g(x),
∴g(x)为奇函数.
设当x=a时g(x)有最大值g(a),则当x=-a时,g(x)有最小值g(-a)=-g(a)
∵f(x)=1+g(x),
∴当x=a时f(x)有最大值g(a)+1,则当x=-a时,g(x)有最小值-g(a)+1
即M=g(a)+1,m=-g(a)+1,
∴M+m=2
故答案为2
点评:本题主要考查利用函数的奇偶性求函数的最大值与最小值,因为f(x)不具有奇偶性,可以通过变形,使f(x)变为一个奇函数加上一个常数的形式.
 变形为
变形为 ,令
,令 ,,可判断函数g(x)的奇偶性,据此找到
,,可判断函数g(x)的奇偶性,据此找到g(x)的最大值与最小值之间的关系,在有f(x)=1+g(x),求出f(x)的最大值与最小值之和.
解答:解:函数
 可变形为
可变形为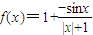
令
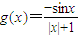 ,,则
,,则 =-g(x),
=-g(x),∴g(x)为奇函数.
设当x=a时g(x)有最大值g(a),则当x=-a时,g(x)有最小值g(-a)=-g(a)
∵f(x)=1+g(x),
∴当x=a时f(x)有最大值g(a)+1,则当x=-a时,g(x)有最小值-g(a)+1
即M=g(a)+1,m=-g(a)+1,
∴M+m=2
故答案为2
点评:本题主要考查利用函数的奇偶性求函数的最大值与最小值,因为f(x)不具有奇偶性,可以通过变形,使f(x)变为一个奇函数加上一个常数的形式.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
 (x∈R)的最大值为M,最小值为m,则M+m的值为 .
(x∈R)的最大值为M,最小值为m,则M+m的值为 . (x∈R)的图象为曲线C.
(x∈R)的图象为曲线C. (x∈R)的图象为曲线C.
(x∈R)的图象为曲线C. (x∈R)的图象为曲线C.
(x∈R)的图象为曲线C.