题目内容
双曲线 的两个焦点为F1、F2,点P在双曲线上,若∠F1PF2=60°,则点P到x轴的距离为 .
的两个焦点为F1、F2,点P在双曲线上,若∠F1PF2=60°,则点P到x轴的距离为 .
【答案】分析:由题意可得 F2(5,0),F1 (-5,0),由余弦定理可得 PF1•PF2=64,由 PF1•PF2sin60°
PF1•PF2sin60°
= ×10•|yp|,求得|yp|的值,即为所求.
×10•|yp|,求得|yp|的值,即为所求.
解答:解:由题意可得 F2(5,0),F1 (-5,0),由余弦定理可得 100=PF12+PF22-2PF1•PF2cos60°
=(PF1-PF2)2+PF1•PF2=36+PF1•PF2,∴PF1•PF2=64.
S△F1PF2= PF1•PF2sin60°=
PF1•PF2sin60°= ×10•|yp|,∴|yp|=
×10•|yp|,∴|yp|= ,
,
故答案为: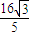 .
.
点评:本题考查双曲线的定义和标准方程,余弦定理,以及双曲线的简单性质的应用,求出PF1•PF2的值,是解题的关键.
 PF1•PF2sin60°
PF1•PF2sin60° =
 ×10•|yp|,求得|yp|的值,即为所求.
×10•|yp|,求得|yp|的值,即为所求.解答:解:由题意可得 F2(5,0),F1 (-5,0),由余弦定理可得 100=PF12+PF22-2PF1•PF2cos60°
=(PF1-PF2)2+PF1•PF2=36+PF1•PF2,∴PF1•PF2=64.
S△F1PF2=
 PF1•PF2sin60°=
PF1•PF2sin60°= ×10•|yp|,∴|yp|=
×10•|yp|,∴|yp|= ,
,故答案为:
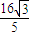 .
.点评:本题考查双曲线的定义和标准方程,余弦定理,以及双曲线的简单性质的应用,求出PF1•PF2的值,是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目