题目内容
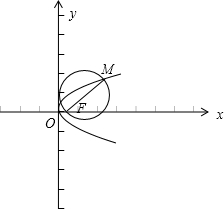
已知点M是抛物线y2=2px（p＞0）上的一点，F为抛物线的焦点，若以|MF|为直径作圆，则这个圆与y轴的关系是
相切
相切
．分析：根据题意，可判断MF的中点到y轴的距离等于|MF|的一半，从而可知圆与y轴的位置关系是相切
解答：解：设圆半径为R
∵F为抛物线y2=2px（p＞0）的焦点，
∴F（
，0）
设M（
，y），MF中点为N（x1，y1）
∴x1=
，y1=
∵|MF|=
+
=
∴
=
=x1=R
∴这个圆与y轴的位置关系是相切．
∵F为抛物线y2=2px（p＞0）的焦点，
∴F（
| p |
| 2 |
设M（
| y2 |
| 2p |
∴x1=
| y2+p2 |
| 4p |
| y |
| 2 |
∵|MF|=
| y2 |
| 2p |
| p |
| 2 |
| y2+p2 |
| 2p |
∴
| |MF| |
| 2 |
| y2+p2 |
| 4p |
∴这个圆与y轴的位置关系是相切．
点评：本题以抛物线为载体，考查抛物线的定义，考查直线与圆的位置关系，属于中档题．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
已知点M是抛物线y2=2px（p＞0）位于第一象限部分上的一点，且点M与焦点F的距离|MF|=2p，则点M的坐标为（ ）
A、（
| ||||
B、（
| ||||
C、（
| ||||
D、（
|