题目内容
 在边长为2的正方形ABCD边上有点P,沿着折线BCDA由点B(起点)向A(终点)运动(不包括B、A两点),设P运动的路程为x,△PAB的面积为y.
在边长为2的正方形ABCD边上有点P,沿着折线BCDA由点B(起点)向A(终点)运动(不包括B、A两点),设P运动的路程为x,△PAB的面积为y.(1)求y关于x的函数关系式y=f(x);
(2)画出函数y=f(x)的图象;
(3)是否存在实数a,使函数y=f(x)的图象关于直线x=a对称?若不存在,则说明理由;若存在,则写出a的值.
分析:(1)由于x=0与x=6时,三点A、B、P不能构成三角形,故这个函数的定义域为(0,6).利用三角形的面积公式能够求出当0<x≤2时,y=f(x)=
•2•x=x;当2<x≤4时,y=f(x)=2;当4<x<6时,y=f(x)=
•2•(6-x)=6-x.由此能够求出这个函数的解析式.
(2)结合f(x)的解析式,利用描点法作图,能够得到其图象.
(3)结合f(x)的图象能够示出a的值.
| 1 |
| 2 |
| 1 |
| 2 |
(2)结合f(x)的解析式,利用描点法作图,能够得到其图象.
(3)结合f(x)的图象能够示出a的值.
解答:解:(1)由于x=0与x=6时,三点A、B、P不能构成三角形,故这个函数的定义域为(0,6).
当0<x≤2时,y=f(x)=
•2•x=x;
当2<x≤4时,y=f(x)=2;
当4<x<6时,y=f(x)=
•2•(6-x)=6-x.
∴这个函数的解析式为
f(x)=
.
(2)结合f(x)=
.
作出其图象如下:

(3)结合f(x)=
的图象知,
函数y=f(x)的图象关于直线x=3对称.
∴a=3.
当0<x≤2时,y=f(x)=
| 1 |
| 2 |
当2<x≤4时,y=f(x)=2;
当4<x<6时,y=f(x)=
| 1 |
| 2 |
∴这个函数的解析式为
f(x)=
|
(2)结合f(x)=
|
作出其图象如下:

(3)结合f(x)=
|
函数y=f(x)的图象关于直线x=3对称.
∴a=3.
点评:本题考查函数解析式的求法、函数图象的画法和函数对称轴的求法,解题时要认真审题,注意分段函数的性质和应用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 在边长为2的正方形ABCD的边上有动点M,从点B开始,沿折线BCDA向A点运动,设M点运动的距离为x,△ABM的面积为S.
在边长为2的正方形ABCD的边上有动点M,从点B开始,沿折线BCDA向A点运动,设M点运动的距离为x,△ABM的面积为S.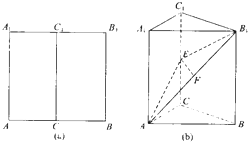 如图(a)所示,在边长为2的正方形ABB1A1中,C,C1分别是AB,A1B1的中点,现将正方形ABB1A1沿CC1折叠,使得平面ACC1A1⊥平面CBB1C1,连接AB,A1B1,AB1,如图(b)所示,F是AB1的中点,E是CC1上的点.
如图(a)所示,在边长为2的正方形ABB1A1中,C,C1分别是AB,A1B1的中点,现将正方形ABB1A1沿CC1折叠,使得平面ACC1A1⊥平面CBB1C1,连接AB,A1B1,AB1,如图(b)所示,F是AB1的中点,E是CC1上的点.