题目内容
设集合M={f(x)|存在实数t使得函数f(x)满足f(t+1)=f(t)+f(1)},则下列函数(a,b,k都是常数):
①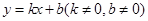 ;②
;②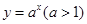 ;③
;③ ;④
;④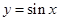 .
.
其中属于集合M的函数是_____(填序号).
②④
解析试题分析:对于①,由k(t+1)+b=kt+b+k+b得b=0,矛盾;
对于②,由at+1=at+a知,可取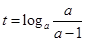 符合题意;
符合题意;
对于③,由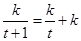 知,无实根;
知,无实根;
对于④,由sin(t+1)=sin t+sin 1知,取t=2kπ,k∈Z符合题意;
综上所述,属于集合M的函数是②④.
考点:新定义题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,若
,若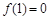 ,则
,则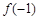 的值为 .
的值为 .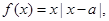 若对任意的
若对任意的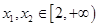 ,且
,且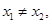
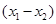
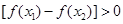 恒成立,则实数a的取值范围为 .
恒成立,则实数a的取值范围为 .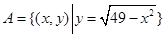 ,
,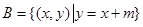 ,且
,且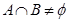 ,则实数
,则实数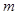 的取值范围是_______________.
的取值范围是_______________. 是奇函数,则常数a=________.
是奇函数,则常数a=________.