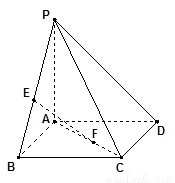题目内容
 (本题满分16分)如图,已知椭圆
(本题满分16分)如图,已知椭圆![]() :
:![]() 的长轴
的长轴![]() 长为4,离心率
长为4,离心率![]() ,
,![]() 为坐标原点,过
为坐标原点,过![]() 的直线
的直线![]() 与
与![]() 轴垂直.
轴垂直.![]() 是椭圆上异于
是椭圆上异于![]() 、
、![]() 的任意一点,
的任意一点,![]() 轴,
轴,![]() 为垂足,延长
为垂足,延长![]() 到点
到点![]() 使得
使得![]() ,连结
,连结![]() 延长交直线
延长交直线![]() 于点
于点![]() ,
,![]() 为
为![]() 的中点.
的中点.
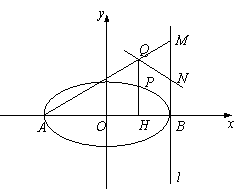 (1)求椭圆
(1)求椭圆![]() 的方程;w ww.ks 5u.co m
的方程;w ww.ks 5u.co m
(2)证明![]() 点在以
点在以![]() 为直径的圆
为直径的圆![]() 上;
上;
(3)试判断直线![]() 与圆
与圆![]() 的位置关系.
的位置关系.
解:(1)由题设可得![]() ,解得
,解得![]() ,所以
,所以 ![]() 所以 椭圆
所以 椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,则
,则![]() .
.
因为 ![]() ,所以
,所以 ![]() .所以
.所以 ![]() .所以
.所以 ![]() 点在以
点在以![]() 为圆心,2为半径的的圆上.即
为圆心,2为半径的的圆上.即![]() 点在以
点在以![]() 为直径的圆
为直径的圆![]() 上.
上.
(3)设![]()
![]() ,则
,则![]() ,且
,且![]() .
.
又![]() ,所以 直线
,所以 直线![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得![]() .又
.又![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以 ![]() .
.
所以 ![]() ,
,![]() .
.
所以 ![]()
![]() .
.
所以 ![]() .所以 直线
.所以 直线![]() 与圆
与圆![]() 相切.
相切.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 所在平面与正
所在平面与正 所在平面互相垂直,
所在平面互相垂直, 分别为
分别为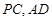 的中点.
的中点.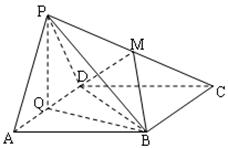
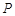 -
- 的体积;
的体积;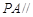 平面
平面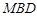 ;
;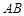 上是否存在一点
上是否存在一点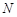 ,使得平面
,使得平面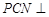 平面
平面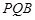 ?若存在,试指出点
?若存在,试指出点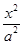 +
+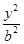 =1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,
=1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,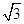 ,
,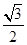 )在椭圆C上,直线l为椭圆C的左准线.
)在椭圆C上,直线l为椭圆C的左准线.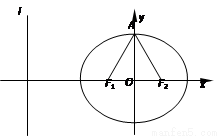
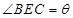 ,试将此人按上述路线从A到C所需时间T表示为
,试将此人按上述路线从A到C所需时间T表示为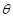 的函数;并求自变量
的函数;并求自变量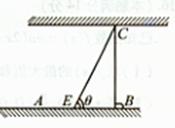
 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.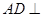 平面
平面 ;
; 与
与 所成的角的大小;
所成的角的大小; 的大小.
的大小.
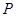 是正方形
是正方形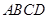 所在平面外一点,
所在平面外一点,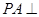 平面
平面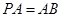 ,点
,点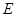 、
、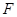 分别在线段
分别在线段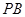 、
、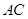 上,满足
上,满足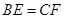 .
.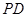 与平面
与平面 ;
;