题目内容
函数f(x)=Acos2(ωx+φ)+1(A>0,ω>0,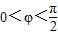 )的最大值为3,它的图象相邻的两个对称轴之间的距离为2,图象在y轴交点的坐标为(0,2),
)的最大值为3,它的图象相邻的两个对称轴之间的距离为2,图象在y轴交点的坐标为(0,2),(1)求函数f(x)的解析式;
(2)设数列an=f(n)(n∈N*),Sn是它的前n项和,求S100.
【答案】分析:(1)先将原函数用降幂公式转化为一个角的一个三角函数的形式,由相邻两对称轴间的距离为2可知周期求得ω,由最大值为3,求得A,又由图象经过点(0,2),求得φ,进而得f(x)解析式.
(2)求出数列的前几项,判断数列是周期数列,求出一个周期的和.然后求解S100.
解答:解:(1)将原函数f(x)=Acos2(ωx+φ)+1转化为:f(x)=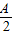 cos(2ωx+2φ)+
cos(2ωx+2φ)+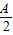 +1
+1
相邻两对称轴间的距离为2可知函数的周期为:4,则2ω=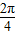 =
=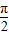 ,ω=
,ω=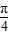
由最大值为3,可知A=2
又∵图象经过点(0,2),
∴cos2φ=0
∴2φ=kπ+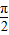 ,
,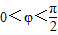 ,φ=
,φ=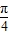 ,
,
∴f(x)=cos(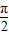 x+
x+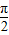 )+2=-sin
)+2=-sin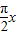 +2.
+2.
(2)∵f(1)=1,f(2)=2,f(3)=3,f(4)=2,f(5)=1…所以数列{an}是周期数列,T=4,
f(1)+f(2)+f(3)+f(4)=8,
S100=f(1)+f(2)+f(3)+…+f(100)=8×25=200.
点评:本题主要考查了降幂公式和三角函数中各参数的意义,由y=Asin(ωx+φ)的部分图象确定其解析式,数列的求和,考查分析问题解决问题的能力.
(2)求出数列的前几项,判断数列是周期数列,求出一个周期的和.然后求解S100.
解答:解:(1)将原函数f(x)=Acos2(ωx+φ)+1转化为:f(x)=
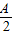 cos(2ωx+2φ)+
cos(2ωx+2φ)+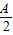 +1
+1相邻两对称轴间的距离为2可知函数的周期为:4,则2ω=
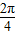 =
=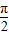 ,ω=
,ω=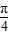
由最大值为3,可知A=2
又∵图象经过点(0,2),
∴cos2φ=0
∴2φ=kπ+
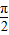 ,
,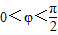 ,φ=
,φ=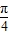 ,
,∴f(x)=cos(
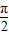 x+
x+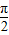 )+2=-sin
)+2=-sin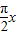 +2.
+2.(2)∵f(1)=1,f(2)=2,f(3)=3,f(4)=2,f(5)=1…所以数列{an}是周期数列,T=4,
f(1)+f(2)+f(3)+f(4)=8,
S100=f(1)+f(2)+f(3)+…+f(100)=8×25=200.
点评:本题主要考查了降幂公式和三角函数中各参数的意义,由y=Asin(ωx+φ)的部分图象确定其解析式,数列的求和,考查分析问题解决问题的能力.

练习册系列答案
相关题目