题目内容
设复数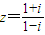
（i为虚数单位），则C8+C81•z+C82•z2+C83•z3+C84•z4+C85•z5+C86•z6+C87•z7=（ ）A．16
B．15
C．16i
D．16-i
【答案】分析：先利用复数的运算求出z=i；再结合二项式定理的应用把所求问题转化为（1+i）8-C88z8即可求出结论．
解答：解：∵z=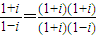
=i．
∵（1+z）8=（1+i）8=C8+C81•z+C82•z2+C83•z3+C84•z4+C85•z5+C86•z6+C87•z7+c88z8．
∴C8+C81•z+C82•z2+C83•z3+C84•z4+C85•z5+C86•z6+C87•z7
=（1+i）8-C88z8
=（1+i）8-C88i8
=[（1+i）4]2-[（i）4]2
=（-4）2-12=15．
故选：B．
点评：本题主要考查二项式定理的应用以及复数的运算．考查计算能力，属于基础题目．解决问题的关键在于把所求问题转化为（1+i）8-C88z8．
解答：解：∵z=
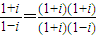=i．∵（1+z）8=（1+i）8=C8+C81•z+C82•z2+C83•z3+C84•z4+C85•z5+C86•z6+C87•z7+c88z8．
∴C8+C81•z+C82•z2+C83•z3+C84•z4+C85•z5+C86•z6+C87•z7
=（1+i）8-C88z8
=（1+i）8-C88i8
=[（1+i）4]2-[（i）4]2
=（-4）2-12=15．
故选：B．
点评：本题主要考查二项式定理的应用以及复数的运算．考查计算能力，属于基础题目．解决问题的关键在于把所求问题转化为（1+i）8-C88z8．
练习册系列答案
相关题目
其中i为虚数单位，
∈R，则|z|的取值范围是
]
，3]
，
]
]
其中i为虚数单位，
，则|z|的取值范围是
]
]
，
]
，
]
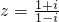（i为虚数单位），则C80+C81•z+C82•z2+C83•z3+C84•z4+C85•z5+C86•z6+C87•z7=
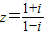（i为虚数单位），则C8+C81•z+C82•z2+C83•z3+C84•z4+C85•z5+C86•z6+C87•z7=（ ）