题目内容
(1)证明:当x∈[0,1]时,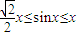 ;
;(2)若不等式
 对x∈[0,1]恒成立,求实数a的取值范围.
对x∈[0,1]恒成立,求实数a的取值范围.
【答案】分析:(1)记F(x)=sinx-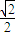 x,可求得F′(x)=cosx-
x,可求得F′(x)=cosx- ,分x∈(0,
,分x∈(0, )与x∈(
)与x∈( ,1)两类讨论,可证得当x∈[0,1]时,F(x)≥0,即sinx≥
,1)两类讨论,可证得当x∈[0,1]时,F(x)≥0,即sinx≥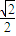 x;记H(x)=sinx-x,同理可证当x∈(0,1)时,sinx≤x,二者结合即可证得结论;
x;记H(x)=sinx-x,同理可证当x∈(0,1)时,sinx≤x,二者结合即可证得结论;
(2)利用(1),可求得当x∈[0,1]时,ax+x2+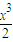 +2(x+2)cosx-4≤(a+2)x,分a≤-2与a>-2讨论即可求得实数a的取值范围.
+2(x+2)cosx-4≤(a+2)x,分a≤-2与a>-2讨论即可求得实数a的取值范围.
解答:(1)证明:记F(x)=sinx- x,则F′(x)=cosx-
x,则F′(x)=cosx-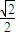 .
.
当x∈(0,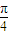 )时,F′(x)>0,F(x)在[0,
)时,F′(x)>0,F(x)在[0,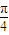 ]上是增函数;
]上是增函数;
当x∈(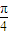 ,1)时,F′(x)<0,F(x)在[
,1)时,F′(x)<0,F(x)在[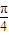 ,1]上是减函数;
,1]上是减函数;
又F(0)=0,F(1)>0,所以当x∈[0,1]时,F(x)≥0,即sinx≥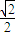 x…3
x…3
记H(x)=sinx-x,则当x∈(0,1)时,H′(x)=cosx-1<0,所以H(x)在[0,1]上是减函数;则H(x)≤H(0)=0,
即sinx≤x.
综上,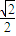 x≤sinx≤x…5
x≤sinx≤x…5
(2)∵当x∈[0,1]时,ax+x2+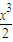 +2(x+2)cosx-4
+2(x+2)cosx-4
=(a+2)x+x2+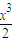 -4(x+2)
-4(x+2)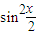
≤(a+2)x+x2+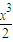 -4(x+2)
-4(x+2)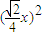
=(a+2)x,
∴当a≤-2时,不等式ax+x2+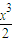 +2(x+2)cosx≤4对x∈[0,1]恒成立,…9
+2(x+2)cosx≤4对x∈[0,1]恒成立,…9
下面证明,当a>-2时,不等式ax+x2+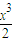 +2(x+2)cosx≤4对x∈[0,1]不恒成立.
+2(x+2)cosx≤4对x∈[0,1]不恒成立.
∵当x∈[0,1]时,ax+x2+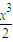 +2(x+2)cosx-4
+2(x+2)cosx-4
=(a+2)x+x2+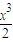 -4(x+2)
-4(x+2)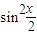
≥(a+2)x+x2+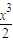 -4(x+2)
-4(x+2)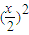
=(a+2)x-x2-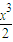
≥(a+2)x- x2
x2
=- x[x-
x[x- (a+2)].
(a+2)].
所以存在x∈(0,1)(例如x取 和
和 中的较小值)满足
中的较小值)满足
ax+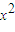 +
+ +2(x+2)cosx-4>0,
+2(x+2)cosx-4>0,
即当a>-2时,不等式ax+x2+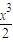 +2(x+2)cosx≤4对x∈[0,1]不恒成立.
+2(x+2)cosx≤4对x∈[0,1]不恒成立.
综上,实数a的取值范围是(-∞,-2].
点评:本题考查不等式的证明,突出考查利用导数研究函数的单调性及函数恒成立问题,考查分类讨论思想与等价转化思想的综合应用,属于难题.
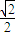 x,可求得F′(x)=cosx-
x,可求得F′(x)=cosx- ,分x∈(0,
,分x∈(0, )与x∈(
)与x∈( ,1)两类讨论,可证得当x∈[0,1]时,F(x)≥0,即sinx≥
,1)两类讨论,可证得当x∈[0,1]时,F(x)≥0,即sinx≥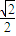 x;记H(x)=sinx-x,同理可证当x∈(0,1)时,sinx≤x,二者结合即可证得结论;
x;记H(x)=sinx-x,同理可证当x∈(0,1)时,sinx≤x,二者结合即可证得结论;(2)利用(1),可求得当x∈[0,1]时,ax+x2+
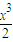 +2(x+2)cosx-4≤(a+2)x,分a≤-2与a>-2讨论即可求得实数a的取值范围.
+2(x+2)cosx-4≤(a+2)x,分a≤-2与a>-2讨论即可求得实数a的取值范围.解答:(1)证明:记F(x)=sinx-
 x,则F′(x)=cosx-
x,则F′(x)=cosx-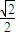 .
.当x∈(0,
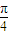 )时,F′(x)>0,F(x)在[0,
)时,F′(x)>0,F(x)在[0,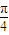 ]上是增函数;
]上是增函数;当x∈(
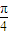 ,1)时,F′(x)<0,F(x)在[
,1)时,F′(x)<0,F(x)在[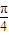 ,1]上是减函数;
,1]上是减函数;又F(0)=0,F(1)>0,所以当x∈[0,1]时,F(x)≥0,即sinx≥
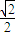 x…3
x…3记H(x)=sinx-x,则当x∈(0,1)时,H′(x)=cosx-1<0,所以H(x)在[0,1]上是减函数;则H(x)≤H(0)=0,
即sinx≤x.
综上,
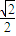 x≤sinx≤x…5
x≤sinx≤x…5(2)∵当x∈[0,1]时,ax+x2+
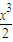 +2(x+2)cosx-4
+2(x+2)cosx-4=(a+2)x+x2+
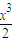 -4(x+2)
-4(x+2)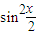
≤(a+2)x+x2+
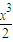 -4(x+2)
-4(x+2)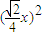
=(a+2)x,
∴当a≤-2时,不等式ax+x2+
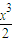 +2(x+2)cosx≤4对x∈[0,1]恒成立,…9
+2(x+2)cosx≤4对x∈[0,1]恒成立,…9下面证明,当a>-2时,不等式ax+x2+
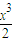 +2(x+2)cosx≤4对x∈[0,1]不恒成立.
+2(x+2)cosx≤4对x∈[0,1]不恒成立.∵当x∈[0,1]时,ax+x2+
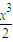 +2(x+2)cosx-4
+2(x+2)cosx-4=(a+2)x+x2+
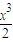 -4(x+2)
-4(x+2)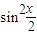
≥(a+2)x+x2+
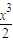 -4(x+2)
-4(x+2)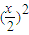
=(a+2)x-x2-
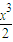
≥(a+2)x-
 x2
x2=-
 x[x-
x[x- (a+2)].
(a+2)].所以存在x∈(0,1)(例如x取
 和
和 中的较小值)满足
中的较小值)满足ax+
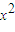 +
+ +2(x+2)cosx-4>0,
+2(x+2)cosx-4>0,即当a>-2时,不等式ax+x2+
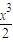 +2(x+2)cosx≤4对x∈[0,1]不恒成立.
+2(x+2)cosx≤4对x∈[0,1]不恒成立.综上,实数a的取值范围是(-∞,-2].
点评:本题考查不等式的证明,突出考查利用导数研究函数的单调性及函数恒成立问题,考查分类讨论思想与等价转化思想的综合应用,属于难题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
