题目内容
如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=![]() .
.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角P—CD—B的大小;
(Ⅲ)求点C到平面PBD的距离.

(1)证明见解析(2)450(3)![]()
解析:
方法一:
 证:(Ⅰ)在Rt△BAD中,AD=2,BD=
证:(Ⅰ)在Rt△BAD中,AD=2,BD=![]() ,
,
∴AB=2,ABCD为正方形,
因此BD⊥AC.
∵PA⊥平面ABCD,BD??平面ABCD,
∴BD⊥PA .
又∵PA∩AC=A
∴BD⊥平面PAC.
解:(Ⅱ)由PA⊥面ABCD,知AD为PD在平面ABCD的射影,又CD⊥AD,
∴CD⊥PD,知∠PDA为二面角P—CD—B的平面角.
又∵PA=AD,
∴∠PDA=450 .
(Ⅲ)∵PA=AB=AD=2
∴PB=PD=BD=![]()
设C到面PBD的距离为d,由![]() ,
,
有![]() ,
,
 即
即![]() ,
,
得![]()
方法二:
证:(Ⅰ)建立如图所示的直角坐标系,
则A(0,0,0)、D(0,2,0)、P(0,0,2).
在Rt△BAD中,AD=2,BD=![]() ,
,
∴AB=2.
∴B(2,0,0)、C(2,2,0),
∴![]()
∵![]()
即BD⊥AP,BD⊥AC,又AP∩AC=A,
∴BD⊥平面PAC.
解:(Ⅱ)由(Ⅰ)得![]() .
.
设平面PCD的法向量为![]() ,则
,则![]() ,
,
即![]() ,∴
,∴![]()
故平面PCD的法向量可取为![]()
∵PA⊥平面ABCD,∴![]() 为平面ABCD的法向量.
为平面ABCD的法向量.
设二面角P—CD—B的大小为q,依题意可得 ,
,
∴q = 450 .
(Ⅲ)由(Ⅰ)得![]()
设平面PBD的法向量为![]() ,则
,则![]() ,
,
即![]() ,∴x=y=z
,∴x=y=z
故平面PBD的法向量可取为![]() .
.
∵![]() ,
,
∴C到面PBD的距离为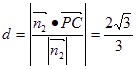

 如图三棱锥P-ABC中,平面PAB⊥平面ABC,AC⊥BC,BC=
如图三棱锥P-ABC中,平面PAB⊥平面ABC,AC⊥BC,BC= 如图三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D为PA的中点,二面角P-AC-B为120°,PC=2,AB=
如图三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D为PA的中点,二面角P-AC-B为120°,PC=2,AB= 如图三棱锥P-ABC,已知PC⊥平面ABC,CD⊥面PAB,BA=BC,PC=AC=2.
如图三棱锥P-ABC,已知PC⊥平面ABC,CD⊥面PAB,BA=BC,PC=AC=2. 如图三棱锥P-ABC中,△PAC,△ABC是等边三角形.
如图三棱锥P-ABC中,△PAC,△ABC是等边三角形.