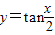题目内容
在下列函数中,同时满足①在(0,
)上递增,②以2π为周期,③是奇函数的函数是( )
| π |
| 2 |
分析:根据已知中的三个条件①在(0,
)上递增,②以2π为周期,③是奇函数,我们结合正弦型函数的性质及正切型函数的性质,逐一分析四个答案中的函数,即可得到答案.
| π |
| 2 |
解答:解:A中y=sin(x+π)=-sinx,在(0,
)上是减函数不满足①;故错;
B中y=cosx,为偶函数且在(0,
)上是减函数,①③条件均不满足;错;
C中y=tan
,为奇函数且在(0,
)上是增函数又是以2π为最小正周期的函数,三个条件均满足;正确;
D中y=-tanx以π为周期,不满足条件②;错
故选C.
| π |
| 2 |
B中y=cosx,为偶函数且在(0,
| π |
| 2 |
C中y=tan
| x |
| 2 |
| π |
| 2 |
D中y=-tanx以π为周期,不满足条件②;错
故选C.
点评:本题考查的知识点是正切函数的周期性、正切函数的单调性、正弦函数的周期性、正弦函数的单调性,其中弦函数的周期T=
,切函数的周期T=
,是我们求解函数周期最常用的办法.
| 2π |
| ω |
| π |
| ω |

练习册系列答案
相关题目
 上递增,②以2π为周期,③是奇函数的函数是
上递增,②以2π为周期,③是奇函数的函数是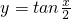
 上递增,②以2π为周期,③是奇函数的函数是( )
上递增,②以2π为周期,③是奇函数的函数是( )