题目内容
已知z1,z2∈C且|z1|=1.若z1+z2=2i,则|z1-z2|的最大值是( )A.6
B.5
C.4
D.3
【答案】分析:根据z1+z2=2i,设出两个复数,两个复数的实部互为相反数,虚部之和是2,表示出两个复数的差的模,用b表示式子中的a,c,复数的模变化为一次函数的平方根,根据一次函数的单调性得到最大值.
解答:解:设出复数z1=a+bi,z2=-a+ci,
∵|z1|=1
∴a2+b2=1,①
∴-1≤b≤1
b+c=2,
|z1-z2|= =
=
=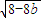
∴当b=-1时,|z1-z2|取到最大值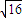 =4,
=4,
故选C.
点评:本题考查复数求模,考查复数之间的关系,考查函数的最值的求法,是一个综合题目,这个复数的问题比较其他的复数问题要麻烦,注意运算不要出错.
解答:解:设出复数z1=a+bi,z2=-a+ci,
∵|z1|=1
∴a2+b2=1,①
∴-1≤b≤1
b+c=2,
|z1-z2|=
 =
=
=
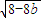
∴当b=-1时,|z1-z2|取到最大值
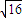 =4,
=4,故选C.
点评:本题考查复数求模,考查复数之间的关系,考查函数的最值的求法,是一个综合题目,这个复数的问题比较其他的复数问题要麻烦,注意运算不要出错.

练习册系列答案
相关题目
已知z1,z2∈C且|z1|=1.若z1+z2=2i,则|z1-z2|的最大值是( )
| A、6 | B、5 | C、4 | D、3 |