题目内容
对n∈N*,不等式
|
(1)求xn,yn;
(2)数列{an}满足a1=x1且n≥2时,an=yn(
| 1 |
| 2y1 |
| 1 |
| 2y2 |
| 1 |
| 2y3 |
| 1 |
| 2yn |
(3)设c1=1,当n≥2时,cn=lg[2
| y | 2 _ |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
分析:(1)画出可行域,结合图形写出xn,yn
(2)利用等比数列的前n项和公式求出an;利用错位相减法和等差数列的前n项和公式求出Sn
(3)先化简Cn,再利用裂项相消法求出T99
(2)利用等比数列的前n项和公式求出an;利用错位相减法和等差数列的前n项和公式求出Sn
(3)先化简Cn,再利用裂项相消法求出T99
解答: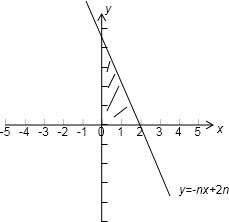 解:(1)
解:(1)
的可行域为
如图示,xn=1,yn=n
(2)由题意可知:a1=1,an=n(
+
+
++
)
故an=n(1-
)=n-
记cn=
,则S′n=1×
+2×
+3×
++n×
S′n=1×
+2×
+3×
++n×
两式相减得:
S′n=
+(
+
+
++
)-n×
S′n=
-n×
=1-
-n×
故S′n=2-(2+n)
故数列{an}的前n项的和为:Sn=
+2-(2+n)
(3)当n≥2时,cn=lg[2(1-
)(1-
)(1-
)(1-
)]
=lg[2×
×
×
××
×
]
=lg
=lg(n+1)-lgn
T99=1+(lg3-lg2)+(lg4-lg3)+(lg5-lg3)++(lg100-lg99)
=1+2-lg2
=3-lg2.
 解:(1)
解:(1)
|
如图示,xn=1,yn=n
(2)由题意可知:a1=1,an=n(
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
故an=n(1-
| 1 |
| 2n |
| n |
| 2n |
记cn=
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 22 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n+1 |
两式相减得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| ||||
1-
|
| 1 |
| 2n+1 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
故S′n=2-(2+n)
| 1 |
| 2n |
故数列{an}的前n项的和为:Sn=
| n(n+1) |
| 2 |
| 1 |
| 2n |
(3)当n≥2时,cn=lg[2(1-
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| n2 |
=lg[2×
| 1×3 |
| 22 |
| 2×4 |
| 32 |
| 3×5 |
| 42 |
| (n-2)n |
| (n-1)2 |
| (n-1)(n+1) |
| n2 |
=lg
| n+1 |
| n |
T99=1+(lg3-lg2)+(lg4-lg3)+(lg5-lg3)++(lg100-lg99)
=1+2-lg2
=3-lg2.
点评:本题考查画不等式组表示的平面区域;数列求和的方法:错位相减法、公式法、裂项相消法.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目