题目内容
对于两条不相交的空间直线 和
和 ,必定存在平面
,必定存在平面 ,使得 ( )
,使得 ( )
A. | B. | C. | D. |
D
解析试题分析:∵空间直线a和b不相交
∴a、b的位置关系可能是平行或异面
再对各选项分别判断:
对于A,当a、b异面时,不存在平面 ,
,
使a?α,b?α,故A不正确;
对于B,若要a⊥ ,b⊥
,b⊥ 都成立,必须a、b互相平行,
都成立,必须a、b互相平行,
所以当a、b不平行时,不存在平面 ,
,
使a⊥ ,b⊥
,b⊥ 都成立,故B不正确;
都成立,故B不正确;
对于C,若要a?α,b⊥ 成立,必须a、b互相垂直,
成立,必须a、b互相垂直,
也就是所成的角为90°时,才存在平面 使a?α,b⊥
使a?α,b⊥ 成立,
成立,
但a、b平行或异面,异面时也不一定成90°角,故C不正确;
对于D,由于a、b的位置关系可能是平行或异面,
①当a、b平行时,很容易找到经过a的平面,但不经过b,可得b∥ ;
;
②当a、b异面时,可以在直线a上取一点O,经过O作直线c使c∥b,
设a、c确定的平面为 ,则直线a?α,b∥
,则直线a?α,b∥ 成立,
成立,
综上所述,只有D项是正确的.
考点:平面的基本性质及推论.
点评:本题借助于一个平面存在的问题,着重考查了平面的基本性质、直线与平面平行的判定定理和直线与平面垂直的定义与性质等知识点,属于基础题.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案设
 是两条直线,
是两条直线, 是两个平面,则
是两个平面,则 的一个充分条件是( )
的一个充分条件是( )
A. | B. |
C. | D. |
已知m、n是两条不重合的直线,α、β是两个不重合的平面,下列命题中正确的是( )
| A.若m∥α,n∥β,α∥β,则m∥n | B.若m∥n,nÌα,m(/α,则m∥α |
| C.若α⊥β,m⊥α,则m∥β | D.若m⊥α,nÌβ,m⊥n,则α⊥β |
如图,在长方形ABCD中,AB=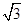 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( )
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( ) 

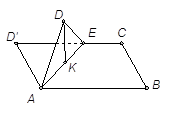
A. | B. | C. | D. |
如图,△ABC中,∠ACB=90°,直线l过点A且垂直于平面ABC,动点P∈l,当点P逐渐远离点A时,∠PCB的大小( ).
| A.变大 | B.变小 | C.不变 | D.有时变大有时变小 |
已知平面 ,直线
,直线 ,直线
,直线 ,有下面四个命题:
,有下面四个命题:
(1)  ∥
∥

 (2)
(2) 


 ∥
∥
(3)  ∥
∥


 (4)
(4) 

 ∥
∥
其中正确的是( )
| A.(1)与(2) | B.(3)与(4) | C.(1)与(3) | D.(2)与(4) |
若a,b是两条直线,α是一个平面,则下列命题正确的是( )
| A.若a∥b,则a平行于经过b的任何平面 |
| B.若a∥α,则a与α内任何直线平行 |
| C.若a∥α,b∥α,则a∥b |
D.若a∥b,a∥α,b α,则b∥α α,则b∥α |
如图,平行六面体 中,侧棱
中,侧棱 长为3,底面是边长为2的菱形,
长为3,底面是边长为2的菱形,
 点E在棱
点E在棱 上,则
上,则 的最小值为( )
的最小值为( )
A. | B.5 | C. | D.7 |
已知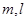 是两条不同的直线,
是两条不同的直线,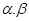 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题:
①若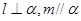 ,则
,则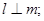 ②若
②若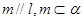 则
则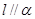 ;
;
③若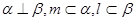 则
则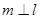 ; ④若
; ④若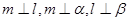 则
则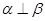 ;
;
其中正确命题的个数为 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |