题目内容
定义在R上的函数f(x)及其导函数f'(x)的图像都是连续不断的曲线,且对于实数a, b (a<b)有f'(a)>0,f'(b)<0,现给出如下结论:
①$x0∈[a,b],f(x0)=0;②$x0∈[a,b],f(x0)>f(b);
③"x0∈[a,b],f(x0)>f(a);④$x0∈[a,b],f(a)-f(b)>f' x0)(a-b).
其中结论正确的有 。
【答案】
②④
【解析】
试题分析:定义在R上的函数 及其导函数
及其导函数 的图象都是连续不断的曲线,且对于实数
的图象都是连续不断的曲线,且对于实数 ,有
,有 ,说明在区间
,说明在区间 内存在
内存在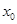 ,使
,使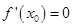 ,所以函数
,所以函数 在区间
在区间 内有极大值点,同时说明函数在区间
内有极大值点,同时说明函数在区间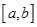 内至少有一个增区间和一个减区间.由上面的分析可知,函数
内至少有一个增区间和一个减区间.由上面的分析可知,函数 在区间
在区间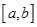 上不一定有零点,故①不正确;因为函数在区间
上不一定有零点,故①不正确;因为函数在区间 内有极大值点,与实数
内有极大值点,与实数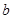 在同一个减区间内的极大值点的横坐标就是存在的一个
在同一个减区间内的极大值点的横坐标就是存在的一个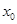 ,所以②正确;函数
,所以②正确;函数 在区间
在区间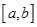 的两个端点处的函数值无法判断大小,若
的两个端点处的函数值无法判断大小,若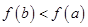 ,取
,取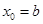 ,则③不正确;当
,则③不正确;当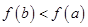 ,且
,且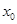 是极大值点的横坐标时结论④正确.
是极大值点的横坐标时结论④正确.
考点:利用导数研究函数的单调性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目