题目内容
已知x=-1是![]() 的一个极值点
的一个极值点
(1)求![]() 的值;
的值;
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)设![]() ,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由。
,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由。
b= -1; 单调增区间为![]() ,过点(2,5)可作2条曲线y=g(x)的切线
,过点(2,5)可作2条曲线y=g(x)的切线
解析:
解:(1) 因x=-1是![]() 的一个极值点 ∴
的一个极值点 ∴ ![]() 即 2+b-1=0
即 2+b-1=0
∴b= -1经检验,适合题意,所以b= -1.
(2) ![]() ∴
∴![]() >0 ∴
>0 ∴ ![]() >0 ∴x>
>0 ∴x>![]() ∴函数 的单调增区间为
∴函数 的单调增区间为![]()
(3)![]() =2x+lnx
=2x+lnx
设过点(2,5)与曲线g (x)的切线的切点坐标为![]() ∴
∴![]()
即![]() ∴
∴![]()
令h(x)=![]() ∴
∴![]() =
=![]() =0 ∴
=0 ∴![]()
∴h(x)在(0,2)上单调递减,在(2,![]() )上单调递增
)上单调递增
![]() 又
又![]() ,h(2)=ln2-1<0,
,h(2)=ln2-1<0,![]()
∴h(x)与x轴有两个交点∴过点(2,5)可作2条曲线y=g(x)的切线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

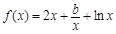 的一个极值点,
的一个极值点, 的值;
的值; 的单调递减区间
的单调递减区间 试问过点(2,5)可作多少条直线与曲线
试问过点(2,5)可作多少条直线与曲线 相切?请说明理由.
相切?请说明理由.