题目内容
设等比数列 的公比为
的公比为 ,前n项和为
,前n项和为 ,若
,若 ,
, ,
, 成等差数列,则公比
成等差数列,则公比 为( ).
为( ).
A. B.
B. C.
C. 或
或 D.
D.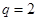 或
或
【答案】
B
【解析】
试题分析:首先由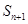 ,
, ,
, 成等差数列,可得2Sn=Sn+1+Sn+2,然后利用等比数列的求和公式分别表示
成等差数列,可得2Sn=Sn+1+Sn+2,然后利用等比数列的求和公式分别表示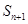 ,
, ,
, 成等差数列,注意分q=1和q≠1两种情况讨论,解方程即可。解:设等比数列{an}的公比为q,前n项和为Sn,且
成等差数列,注意分q=1和q≠1两种情况讨论,解方程即可。解:设等比数列{an}的公比为q,前n项和为Sn,且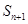 ,
, ,
, 成等差数列,则2Sn=Sn+1+Sn+2,若q=1,则Sn=na1,式显然不成立.
成等差数列,则2Sn=Sn+1+Sn+2,若q=1,则Sn=na1,式显然不成立.
若q≠1,则为
故2qn=qn+1+qn+2,即q2+q-2=0,因此q=-2.故选B.
考点:等差数列
点评:本题主要考查等差数列的定义和性质,等比数列的前n项和公式,涉及等比数列求和时,若公比为字母,则需要分类讨论

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 的公比为q,前n项和为
的公比为q,前n项和为 ,若
,若 ,
, 成等差数列,
成等差数列, 中,对任意
中,对任意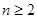 ,
, 时都有
时都有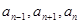 成等差,求公比
成等差,求公比 的值
的值 是等比数列
是等比数列 项和,当
项和,当 成等差时,是否有
成等差时,是否有 一定也成等差数列?说明理由
一定也成等差数列?说明理由 ,使
,使 成等差且
成等差且 也成等差,若存在,求出
也成等差,若存在,求出 }的公比为q,前n项和为
}的公比为q,前n项和为 ,若
,若 ,
, 成等差数列,
成等差数列,