题目内容
对于下列命题:①
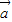 =(-1,1)在
=(-1,1)在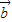 =(3,4)方向上的投影为
=(3,4)方向上的投影为 ;
;②若
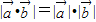 ,则
,则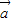 ∥
∥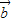 ;
;③在△ABC中,A>B?sinA>sinB;
④若数列{an}{bn}是等比数列,则数列{an+bn}也是等比数列;
⑤在△ABC中,若tanAtanB>1,则△ABC一定是锐角三角形.
以上正确的命题的序号是 .
【答案】分析:①利用向量投影的定义求值.②利用向量的数量积和向量共线的条件判断.③利用正弦定理进行判断.④利用等比数列的心中判断.⑤利用两角和的正切公式或三角函数的性质判断.
解答:解:①根据向量投影的概念可知, =(-1,1)在
=(-1,1)在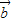 =(3,4)方向上的投影
=(3,4)方向上的投影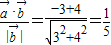 ,所以①正确.
,所以①正确.
②若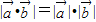 ,当
,当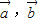 有一个为零向量时,满足
有一个为零向量时,满足 ∥
∥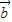 ,当
,当 都不是零向量时,得|cos<
都不是零向量时,得|cos<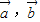 >|=1,所以<
>|=1,所以<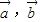 >=0或π,
>=0或π,
所以满足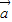 ∥
∥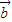 ,所以②正确.
,所以②正确.
③在三角形中,根据正弦定理得A>B?a>b?sinA>sinB,所以③正确.
④若数列{an}{bn}是等比数列,不妨设an=1,bn=-1,但an+bn=1-1=0,所以此时数列{an+bn}不可能是等比数列,所以④错误.
⑤由tanAtanB>1,得tanA>0,tanB>0,所以A,B都是锐角.又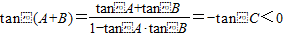 ,所以tanC>0,即C也为锐角,即△ABC一定是锐角三角形,所以⑤正确.
,所以tanC>0,即C也为锐角,即△ABC一定是锐角三角形,所以⑤正确.
故答案为:①②③⑤.
点评:本题主要考查了与向量和三角函数有关的命题的真假判断,综合性较强,涉及的知识点较多.
解答:解:①根据向量投影的概念可知,
 =(-1,1)在
=(-1,1)在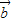 =(3,4)方向上的投影
=(3,4)方向上的投影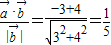 ,所以①正确.
,所以①正确.②若
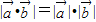 ,当
,当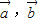 有一个为零向量时,满足
有一个为零向量时,满足 ∥
∥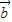 ,当
,当 都不是零向量时,得|cos<
都不是零向量时,得|cos<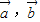 >|=1,所以<
>|=1,所以<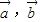 >=0或π,
>=0或π,所以满足
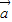 ∥
∥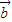 ,所以②正确.
,所以②正确.③在三角形中,根据正弦定理得A>B?a>b?sinA>sinB,所以③正确.
④若数列{an}{bn}是等比数列,不妨设an=1,bn=-1,但an+bn=1-1=0,所以此时数列{an+bn}不可能是等比数列,所以④错误.
⑤由tanAtanB>1,得tanA>0,tanB>0,所以A,B都是锐角.又
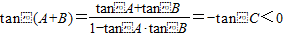 ,所以tanC>0,即C也为锐角,即△ABC一定是锐角三角形,所以⑤正确.
,所以tanC>0,即C也为锐角,即△ABC一定是锐角三角形,所以⑤正确.故答案为:①②③⑤.
点评:本题主要考查了与向量和三角函数有关的命题的真假判断,综合性较强,涉及的知识点较多.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目