Question

已知a是实数，函数f(x)＝x²(x－a)

(1)若f′(1)＝3，求a的值及曲线y＝f(x)在点(1，f(1))处的切线方程；

(2)a>0,求f(x)的单调增区间．

 

Answer 1

【答案】

(1) 3x－y－2＝0

(2) ，

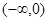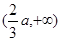
【解析】(1)f′(x)＝3x²－2ax，

因为f′(1)＝3－2a＝3，所以a＝0.又当a＝0时，f(1)＝1，f′(1)＝3，

所以曲线y＝f(x)在点(1，f(1))处的切线方程为3x－y－2＝0． 

(2)令f′(x)＝0，解得x₁＝0，x₂＝，>0，

f(x)在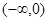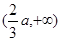，上单调递增．