题目内容
某公园有甲、乙两个相邻景点，原拟定甲景点内有2个A班同学和2个B班同学；乙景点内有2个A班同学和3个B班同学，后由于某种原因，甲、乙两景点各有一个同学交换景点观光．
（1）求甲景点恰有2个A班同学的概率；
（2）求甲景点A班同学数ξ的分布列及数学期望．
（1）求甲景点恰有2个A班同学的概率；
（2）求甲景点A班同学数ξ的分布列及数学期望．
（1）甲、乙两景点各有一个同学交换景点后，甲景点恰有2个A班同学有两种情况
①互换的是A班同学，此时甲景点恰有2个A班的同学的事件记为A1．
P(A1)=
=
②互换的是B班同学，此时甲景点恰有2个A班的同学的事件记为A2．．
P(A2)=
=
所以甲景点恰有2个A班的同学的概率P=P(A1)+P(A2)=
+
=
．
（2）甲景点内A班的同学数为ξ，
则P(ξ=1)=
=
，
P(ξ=2)=
，
P(ξ=3)=
=
所以Eξ=1×
+2×
+3×
=
．
①互换的是A班同学，此时甲景点恰有2个A班的同学的事件记为A1．
P(A1)=
| ||||
|
| 1 |
| 5 |
②互换的是B班同学，此时甲景点恰有2个A班的同学的事件记为A2．．
P(A2)=
| ||||
|
| 3 |
| 10 |
所以甲景点恰有2个A班的同学的概率P=P(A1)+P(A2)=
| 1 |
| 5 |
| 3 |
| 10 |
| 1 |
| 2 |
（2）甲景点内A班的同学数为ξ，
则P(ξ=1)=
| ||||
|
| 3 |
| 10 |
P(ξ=2)=
| 1 |
| 2 |
P(ξ=3)=
| ||||
|
| 1 |
| 5 |
所以Eξ=1×
| 3 |
| 10 |
| 1 |
| 2 |
| 1 |
| 5 |
| 19 |
| 10 |
练习册系列答案
相关题目
的分布列及数学期望。
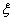的分布列及数学期望。