题目内容
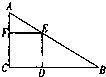如图所示，已知在△ABC中，∠C=90°，正方形DEFC内接于△ABC，DE∥AC，EF∥BC，AC=1，BC=2，则AF：FC=1：2
1：2
．分析：根据平行线分线段成比例定理的推论，我们易判断出△AFE∽△ACB，根据三角形相似的性质，AF：FE=AC：CB=1：2，进而根据四边形DEFC为正方形，即FE=FC，即可得到结论．
解答：解：∵EF∥BC
∴△AFE∽△ACB
∴AF：FE=AC：CB
又∵AC=1，BC=2，四边形DEFC为正方形，即FE=FC
∴AF：FC=AC：CB=1：2
故答案为：1：2
∴△AFE∽△ACB
∴AF：FE=AC：CB
又∵AC=1，BC=2，四边形DEFC为正方形，即FE=FC
∴AF：FC=AC：CB=1：2
故答案为：1：2
点评：本题考查的知识是平行线分线段成比例定理的推论，其中根据平行线分线段成比例定理的推论，得到△AFE∽△ACB，是解答本题的关键．
练习册系列答案
相关题目
，已知在矩形ABCD中，AB=1，BC=a（a＞0），PA⊥平面ABCD，且PA=1．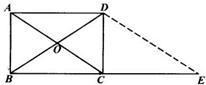
如图所示，已知在矩形ABCD中，
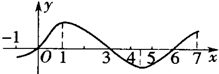设定义在[-1，7]上的函数y=f（x）的图象如图所示．已知（a，b）是
