题目内容
设点O在△ABC的内部且满足：4| OA |
| OB |
| OC |
| 0 |
分析：题中条件：“满足：4
+
+
=
，”说明点O在三角形的位置，由下面的图可知，它在中线的三分之一处；
利用几何概型的意义求两个三角形的面积比即可．
| OA |
| OB |
| OC |
| 0 |
利用几何概型的意义求两个三角形的面积比即可．
解答：解：∵4
+
+
=
，
∴点O在三角形内且在中线的三分之一处，如图：
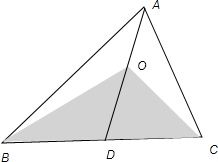
∴豆子落在△OBC中的概率=
=
．
故填：
．
| OA |
| OB |
| OC |
| 0 |
∴点O在三角形内且在中线的三分之一处，如图：
∴豆子落在△OBC中的概率=
| S△OBC |
| S△ABC |
| 2 |
| 3 |
故填：
| 2 |
| 3 |
点评：本题考查几何概型，将基本事件“几何化”，实际问题转化为数学问题，将随机事件的概率抽象为几何概型是研究的关键．
练习册系列答案
名校课堂系列答案
相关题目
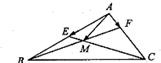在平面向量中有如下定理：设点O、P、Q、R为同一平面内的点，则P、Q、R三点共线的充要条件是：存在实数t，使
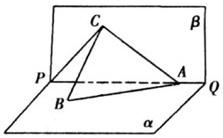如图所示，PQ为平面α、β的交线，已知二面角α-PQ-β为直二面角，A∈PQ，B∈α，C∈β，CA=CB=kAB（k∈R*），∠BAP=45°．
（2011•惠州二模）在平面向量中有如下定理：设点O，P，Q，R为同一平面内的点，则P，Q，R三点共线的充要条件是：存在实数t，使在平面向量中有如下定理：设点O，P，Q，R为同一平面内的点，则P、Q、R三点共线的充要条件是：存在实数t，使
.试利用该定理解答下列问题：如图，
 |
在ΔABC中，点E为AB边的中点，点F在AC边上，且CF＝2FA，BF交CE于点M，设
，则x＋y＝ .
的交线, 已知二面角
为直二面角,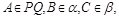 
, ∠BAP＝45°. 
内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心？
时, 求二面角B－AC－P的大小.