题目内容
为了解儿子身高与其父亲身高的关系,随机抽取3对父子的身高数据如表:则y对x的线性回归方程为( )
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据所给的数据计算出x,y的平均数和回归直线的斜率,即可写出回归直线方程.
解答:解:∵
=
(174+176+178)=176,
=
(176+175+177)=176,
∴样本组数据的样本中心点是(176,176),
∴b=
=
,a=
-b
=132,
∴回归直线方程为
=
x+132.
故选:B.
. |
| x |
| 1 |
| 3 |
. |
| y |
| 1 |
| 3 |
∴样本组数据的样本中心点是(176,176),
∴b=
| 174×176+176×175+178×177-3×176×176 |
| 1742+1762+1782-3×1762 |
| 1 |
| 4 |
. |
| y |
. |
| x |
∴回归直线方程为
 |
| y |
| 1 |
| 4 |
故选:B.
点评:本题考查回归分析的初步应用,写方程要用的斜率和x,y的平均数都要经过计算算出,这样的题有一定的运算量,是一个基础题.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
为了解儿子身高与其父亲身高的关系,随机抽取5对父子身高数据如下
则y对x的线性回归方程为( )
| 父亲身高x(cm) | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y(cm) | 175 | 175 | 176 | 177 | 177 |
| A、y=x-1 | ||
| B、y=x+1 | ||
C、y=88+
| ||
| D、y=176 |
.为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如
下: 则y对x的线性回归方程为( )
|
父亲身高x(cm) |
174 |
176 |
176 |
176 |
178 |
|
儿子身高y(cm) |
175 |
175 |
176 |
177 |
177 |
A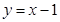 . B.
. B.
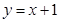 C.
C.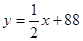 D.
D.