题目内容
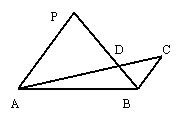
如图在 中,
中,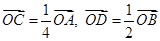 ,
, 与
与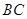 交于
交于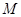 点.设
点.设 .
.
(1)用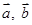 表示
表示 ;
;
(2) 已知线段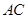 上取一点
上取一点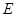 ,在线段
,在线段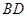 上取一点
上取一点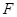 ,使
,使 过点
过点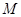 .设
.设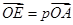 ,
, ,则
,则 是否为定值,如果是定值,这个定值是什么?
是否为定值,如果是定值,这个定值是什么?

【答案】
见解析.
【解析】第一问中,利用向量的加减法法则,可知设则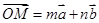
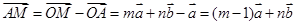
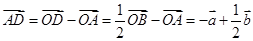 ∵
∵ 三点共线,
三点共线,
∴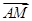 与
与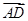 共线,故存在实数
共线,故存在实数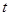 ,使得
,使得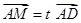 ,即
,即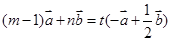 ,
,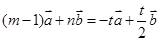 ,得到
,得到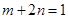
又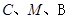 三点共线得到
三点共线得到
∴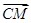 与
与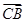 共线,同理可得
共线,同理可得
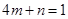
第二问中,∵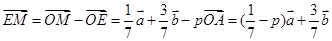 ,
,
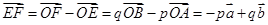 ,
,
又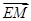 与
与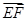 共线,故存在实数
共线,故存在实数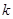 ,使得
,使得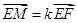 ,即
,即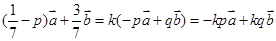 .
.
利用向量相等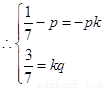 ,得到结论。
,得到结论。
解:(1)设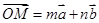 ,则
,则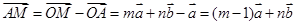 ,
,
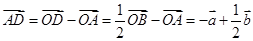 .
.
∵ 三点共线,
三点共线,
∴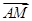 与
与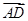 共线,故存在实数
共线,故存在实数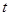 ,使得
,使得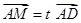 ,即
,即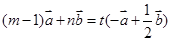 ,
,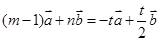 ,
,
∴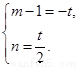 ,消去
,消去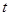 得
得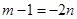 ,即
,即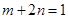 . ①…………………3分
. ①…………………3分
∵ 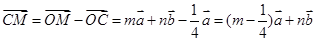 ,
,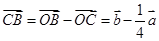 ,
,
又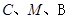 三点共线
三点共线
∴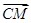 与
与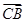 共线,同理可得
共线,同理可得
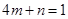 . ②…………………………………6分
. ②…………………………………6分
联立①②,解得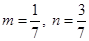 .
.
故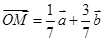 .………………………………………………7分
.………………………………………………7分
(2)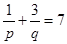 .
.
∵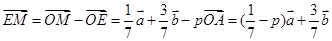 ,
,
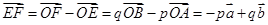 ,
,
又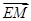 与
与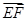 共线,故存在实数
共线,故存在实数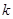 ,使得
,使得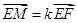 ,即
,即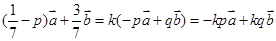 .
.
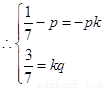 ,消去
,消去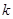 得
得 ,整理得
,整理得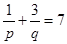 .………………14分
.………………14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 8、如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )
8、如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( ) 的圆心,且垂直于极轴的直线的极坐标
的圆心,且垂直于极轴的直线的极坐标 方程为 。
方程为 。 的不等式
的不等式 是常数)的解是非空集合,则
是常数)的解是非空集合,则 的取
的取 值范围 。
值范围 。 ,
, ,
, 与
与 交于点D,且
交于点D,且 ,
, ,则
,则 。
。 
 .以极点为平面直角坐标系的原点,极轴为x
.以极点为平面直角坐标系的原点,极轴为x 的参数方程是
的参数方程是 ,
, (2)(选修4—5 不等式选讲)已知
(2)(选修4—5 不等式选讲)已知 ,且
,且  ,则
,则 的最小值为 .
的最小值为 . ,
, ,
, 与
与 交于点D,
交于点D, ,
, ,则
,则 .
.