题目内容
设n∈N+且n≥2,证明: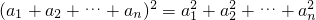 +2[a1(a2+a3+…+an)+a2(a3+a4+…+an)+…+an-1an].
+2[a1(a2+a3+…+an)+a2(a3+a4+…+an)+…+an-1an].
证明:(1)当n=2时,有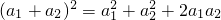 ,命题成立.
,命题成立.
(2)假设当n=k(k≥2)时,命题成立,
即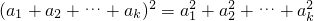 +2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]成立,
+2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]成立,
那么,当n=k+1时,有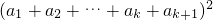 =
=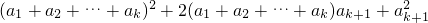
=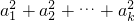 +2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]+2(a1+a2+…
+2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]+2(a1+a2+…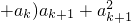
=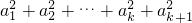 +2[a1(a2+a3+…+ak+ak+1)+a2(a3+a4+…+ak+ak+1)+…+akak+1].
+2[a1(a2+a3+…+ak+ak+1)+a2(a3+a4+…+ak+ak+1)+…+akak+1].
所以当n=k+1时,命题也成立.
根据(1)和(2),可知结论对任意的n∈N*且n≥2都成立.
分析:直接利用数学归纳法的证明步骤证明不等式,(1)验证n=2时不等式成立;(2)假设当n=k(k≥2)时成立,利用上假设证明n=k+1时,不等式也成立.
点评:本题是中档题,考查数学归纳法的证明步骤和方法,注意证明n=k+1时,必须用上假设,这是易错点.
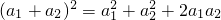 ,命题成立.
,命题成立.(2)假设当n=k(k≥2)时,命题成立,
即
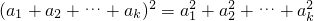 +2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]成立,
+2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]成立,那么,当n=k+1时,有
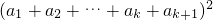 =
=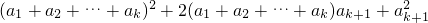
=
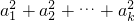 +2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]+2(a1+a2+…
+2[a1(a2+a3+…+ak)+a2(a3+a4+…+ak)+…+ak-1ak]+2(a1+a2+…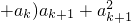
=
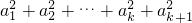 +2[a1(a2+a3+…+ak+ak+1)+a2(a3+a4+…+ak+ak+1)+…+akak+1].
+2[a1(a2+a3+…+ak+ak+1)+a2(a3+a4+…+ak+ak+1)+…+akak+1].所以当n=k+1时,命题也成立.
根据(1)和(2),可知结论对任意的n∈N*且n≥2都成立.
分析:直接利用数学归纳法的证明步骤证明不等式,(1)验证n=2时不等式成立;(2)假设当n=k(k≥2)时成立,利用上假设证明n=k+1时,不等式也成立.
点评:本题是中档题,考查数学归纳法的证明步骤和方法,注意证明n=k+1时,必须用上假设,这是易错点.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 …
… 对一切n∈N*且n≥2恒成立,求实数k的取值范围.
对一切n∈N*且n≥2恒成立,求实数k的取值范围.