题目内容
给出下列命题
①“a>b”是“a2>b2”的充分不必要条件;
②“lga=lgb”是“a=b”的必要不充分条件;
③若x, y∈R,则“|x|=|y|”是“x2=y2”的充要条件;
④△ABC中,“sinA>sinB”是“A>B”的充要条件.
其中真命题是 .(写出所有真命题的序号)
③④
解析试题分析:当a>b时,a2>b2不一定成立,当a2>b2时,a>b也不一定成立,故①为假命题;当lga=lgb时,可以得到a=b,但a=b时,lga=lgb不一定成立,也可能没意义,故②为假命题;当x, y∈R时,若|x|=|y|,则x2=y2成立,若x2=y2成立,则|x|=|y|也成立,故③为真命题;△ABC中,若sinA>sinB成立,由正弦定理 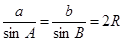 ,所以a>b,所以A>B.反之,若A>B成立,所以a>b,因为a=2RsinA,b=2RsinB,所以sinA>sinB,所以sinA>sinB是A>B的充要条件,故④为真命题。
,所以a>b,所以A>B.反之,若A>B成立,所以a>b,因为a=2RsinA,b=2RsinB,所以sinA>sinB,所以sinA>sinB是A>B的充要条件,故④为真命题。
考点:充分、必要、充要条件的判断;对数的运算;三角形内的隐含条件;正弦定理。
点评:做本题要对四个命题一一进行判断,判断时尤其要考注意特殊情况,考虑周全,否则容易出错。

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目