题目内容
已知椭圆E:
+
=1(a>b>0)的离心率为
,它的上顶点为A,左、右焦点分别为F1,F2,直线AF1,AF2分别交椭圆于点B,C.
(1)求证直线BO平分线段AC;
(2)设点P(m,n)(m,n为常数)在直线BO上且在椭圆外,过P的动直线l与椭圆交于两个不同点M,N,在线段MN上取点Q,满足
=
,试证明点Q恒在一定直线上.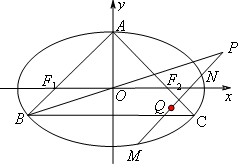
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
(1)求证直线BO平分线段AC;
(2)设点P(m,n)(m,n为常数)在直线BO上且在椭圆外,过P的动直线l与椭圆交于两个不同点M,N,在线段MN上取点Q,满足
| MP |
| NP |
| MQ |
| QN |

证明:(1)由题意,e=
=
,则a=
c,b2=a2-c2=2c2,
故椭圆方程为
+
=1,
即2x2+3y2-6c2=0,其中A(0,
c),F1(-c,0),
∴直线AF1的斜率为
,此时直线AF1的方程为y=
(x+c),
联立
得2x2+3cx=0,解得x1=0(舍)和x2=-
c,即B(-
c,-
c),
由对称性知C(
c,-
c).
直线BO的方程为y=
x,
线段AC的中点坐标为(
c,
),
AC的中点坐标满足直线BO的方程,即直线BO平分线段AC.
(2)设过P的直线l与椭圆交于两个不同点的坐标为M(x1,y1),N(x2,y2),点Q(x,y),
则2
+3
=6c2,2
+3
=6c2.
设
=
=λ,则
=λ
,
=λ
,
求得m=
,x=
,n=
,y=
,
∴mx=
,ny=
,
∴2mx+3ny=
=
=
=6c2,
由于m,n,C为常数,所以点Q恒在直线2mx+3ny-6c2=0上.
| c |
| a |
| ||
| 3 |
| 3 |
故椭圆方程为
| x2 |
| 3c2 |
| y2 |
| 2c2 |
即2x2+3y2-6c2=0,其中A(0,
| 2 |
∴直线AF1的斜率为
| 2 |
| 2 |
联立
|
| 3 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
由对称性知C(
| 3 |
| 2 |
| ||
| 2 |
直线BO的方程为y=
| ||
| 3 |
线段AC的中点坐标为(
| 3 |
| 4 |
| ||
| 4 |
AC的中点坐标满足直线BO的方程,即直线BO平分线段AC.
(2)设过P的直线l与椭圆交于两个不同点的坐标为M(x1,y1),N(x2,y2),点Q(x,y),
则2
| x | 21 |
| y | 21 |
| x | 22 |
| y | 22 |
设
| MP |
| NP |
| MQ |
| QN |
| MP |
| NP |
| MQ |
| QN |
求得m=
| x1-λx2 |
| 1-λ |
| x1+λx2 |
| 1+λ |
| y1-λy2 |
| 1-λ |
| y1+λy2 |
| 1+λ |
∴mx=
| ||||
| 1-λ2 |
| ||||
| 1-λ2 |
∴2mx+3ny=
2
| ||||||||
| 1-λ2 |
2
| ||||||||
| 1-λ2 |
| 6c2-6c2λ2 |
| 1-λ2 |
由于m,n,C为常数,所以点Q恒在直线2mx+3ny-6c2=0上.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 (2012•佛山二模)已知椭圆E:
(2012•佛山二模)已知椭圆E: