题目内容
以下有四种说法:(1)若f′(x)=0,则f(x)在x=x处取得极值;
(2)由变量x和y的数据得到其回归直线方程
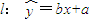 ,则l一定经过点
,则l一定经过点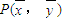 ;
;(3)若p∨q为真,p∧q为假,则p与q必为一真一假;
(4)函数
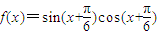 最小正周期为π,其图象的一条对称轴为
最小正周期为π,其图象的一条对称轴为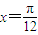 .
.以上四种说法,其中正确说法的序号为 .
【答案】分析:根据函数的极值与导数之间的关系,通过举出反例得到(1)错误;根据线性回归的性质,得到(2)正确;根据含有“或”和“且”等逻辑词的命题真假的判断,得到(3)正确;根据函数y=Asin(ωx+φ)的图象与性质的结论,得到(4)正确.
解答:解:对于(1),若f′(x)=0,则f(x)在x=x处不一定取得极值
反例:函数y=x3在点x=0处满足导数f′(0)=0,
但f(x)在x=0处取没有取得极值,故(1)错误;
对于(2),根据线性回归的性质,若变量x和y满足线性回归特征,
则其平均值点P(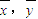 )必定满足线性回归方程
)必定满足线性回归方程 ,
,
即l一定经过点 ,故(2)正确;
,故(2)正确;
对于(3),若p∨q为真,说明p、q当中必定有真命题,
又有p∧q为假,说明p、q当中必定有假命题,
故p与q必为一真一假,故(3)正确;
对于(4),函数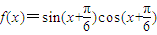 =
=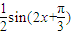
最小正周期为T=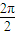 =π,
=π,
再根据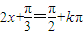 ,k∈Z.得到
,k∈Z.得到
当k=0时,其图象的一条对称轴为 .故(4)正确.
.故(4)正确.
故答案为(2)(3)(4)
点评:本题综合了函数的极值、线性回归方程、逻辑连接词和函数y=Asin(ωx+φ)的图象与性质等知识,考查了命题真假的判断与应用,请同学们注意题中的有关结论,是解题的基本工具,应该多加记忆.
解答:解:对于(1),若f′(x)=0,则f(x)在x=x处不一定取得极值
反例:函数y=x3在点x=0处满足导数f′(0)=0,
但f(x)在x=0处取没有取得极值,故(1)错误;
对于(2),根据线性回归的性质,若变量x和y满足线性回归特征,
则其平均值点P(
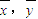 )必定满足线性回归方程
)必定满足线性回归方程 ,
,即l一定经过点
 ,故(2)正确;
,故(2)正确;对于(3),若p∨q为真,说明p、q当中必定有真命题,
又有p∧q为假,说明p、q当中必定有假命题,
故p与q必为一真一假,故(3)正确;
对于(4),函数
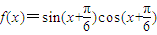 =
=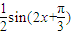
最小正周期为T=
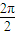 =π,
=π,再根据
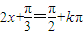 ,k∈Z.得到
,k∈Z.得到
当k=0时,其图象的一条对称轴为
 .故(4)正确.
.故(4)正确.故答案为(2)(3)(4)
点评:本题综合了函数的极值、线性回归方程、逻辑连接词和函数y=Asin(ωx+φ)的图象与性质等知识,考查了命题真假的判断与应用,请同学们注意题中的有关结论,是解题的基本工具,应该多加记忆.

练习册系列答案
相关题目

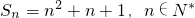 ,则
,则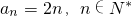 ;
;