题目内容
规定[x]表示不超过x的最大整数,f(x)=
,若方程f(x)=ax+1有且仅有四个实数根,则实数a的取值范围是( )
|
分析:分析函数的特点,作出函数的图象,把问题转化为两函数让图象的交点问题,结合图象由斜率公式可得答案.
解答:解:当x∈[0,+∞)时,f(x)是以1为周期的函数,且f(x)=x-k,x∈[k,k+1)(k∈N),
当x∈(-∞,0)时,f(x)是指数型函数,而y=ax+1为过定点(0,1)斜率为a的直线,
在同一个坐标系中作出它们的图象为:
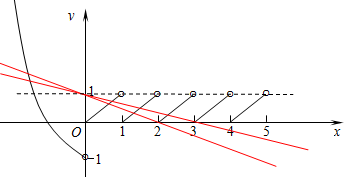
由图象可知,当直线介于两红色线之间时,符合题意,而它们的斜率分别为-
,-
,
故实数a的取值范围为:[-
,-
],
故选B
当x∈(-∞,0)时,f(x)是指数型函数,而y=ax+1为过定点(0,1)斜率为a的直线,
在同一个坐标系中作出它们的图象为:

由图象可知,当直线介于两红色线之间时,符合题意,而它们的斜率分别为-
| 1 |
| 2 |
| 1 |
| 3 |
故实数a的取值范围为:[-
| 1 |
| 2 |
| 1 |
| 3 |
故选B
点评:本题考查根的存在性及个数的判断,数形结合是解决问题的关键,属中档题.

练习册系列答案
相关题目
 ,若方程f(x)=ax+1有且仅有四个实数根,则实数a的取值范围是( )
,若方程f(x)=ax+1有且仅有四个实数根,则实数a的取值范围是( ) B.
B. C.
C. D.
D.