题目内容
袋内装有35个球,每个球上都记有从1到35的一个号码,设号码为n的球重![]() -5n+20克,这些球等可能地从袋中被取出(不受重量和号码等因素的影响),求任意取出的2个球重量相等的概率.
-5n+20克,这些球等可能地从袋中被取出(不受重量和号码等因素的影响),求任意取出的2个球重量相等的概率.
答案:
解析:
解析:
|
解:设第n球与第m球的重量相等,其中n<m,则有 n2-m2-15(n-m)=0,即(n-m)(n+m-15)=0, 所以n=m,或n+m=15. 又因为n<m,所以n+m=15. 若把取2个球的过程视为有序取球,则从袋中的35个球中任取2个球的基本事件有35×34=1190个. 而满足n+m=15的基本事件有:(1,14),(2,13),(3,12),(4,11),…,(14,1),共有14个. 故它们的重量相等的概率为 |

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
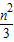 -5n+15克,这些球以等可能性从袋里取出(不受重量、号码的影响).?
-5n+15克,这些球以等可能性从袋里取出(不受重量、号码的影响).?