题目内容
设命题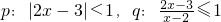
，则p是q的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
A
分析：根据所给的两个命题，对不等式进行求解集，写出两个命题对应的集合，看出两个集合之间的包含关系，得到两个条件之间的关系．
解答：∵p：|2x-3|＜1，
∴p：A{x|1＜x＜2}
∵
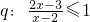
∴（x-1）（x-2）≤0，且x≠2，
∴B={x|1≤x＜2}
∵A⊆B
∴p是q的充分不必要条件，
故选A．
点评：本题考查不等式的求解和必要条件、充分条件与充要条件的判断，本题解题的关键是把命题之间的关系转化为集合之间的包含关系，本题是一个中档题目，注意题目的转化．
分析：根据所给的两个命题，对不等式进行求解集，写出两个命题对应的集合，看出两个集合之间的包含关系，得到两个条件之间的关系．
解答：∵p：|2x-3|＜1，
∴p：A{x|1＜x＜2}
∵
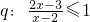
∴（x-1）（x-2）≤0，且x≠2，
∴B={x|1≤x＜2}
∵A⊆B
∴p是q的充分不必要条件，
故选A．
点评：本题考查不等式的求解和必要条件、充分条件与充要条件的判断，本题解题的关键是把命题之间的关系转化为集合之间的包含关系，本题是一个中档题目，注意题目的转化．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，命题
，命题
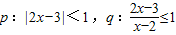，则p是q的
，则p是q的（ ）
，则p是q的（ ）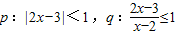
，则p是q的（ ）