题目内容
. (本题满分15分)已知点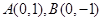 ,
,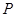 为一个动点,且直线
为一个动点,且直线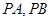 的斜率之积为
的斜率之积为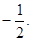
(I)求动点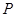 的轨迹
的轨迹 的方程;
的方程;
(II)设 ,过点
,过点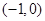 的直线
的直线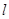 交
交 于
于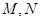 两点,
两点, 的面积记为S,若对满足条件的任意直线
的面积记为S,若对满足条件的任意直线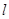 ,不等式
,不等式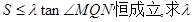 的最小值。
的最小值。
【答案】
(I)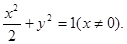 (II)
(II)
【解析】
试题分析:(I)设动点P的坐标为
由条件得 即
即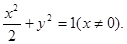
所以动点 的轨迹
的轨迹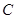 的方程为
的方程为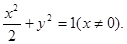 ……6分
……6分
(II)设点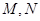 的坐标分别是
的坐标分别是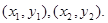
当直线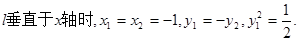
所以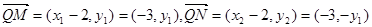
所以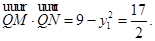
当直线
由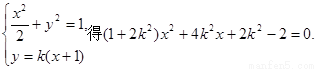 ……8分
……8分
所以
所以
因为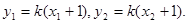
所以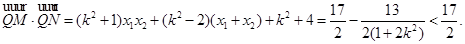
综上所述 ……12分
……12分
因为 恒成立
恒成立
即 恒成立
恒成立
由于 所以
所以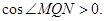
所以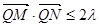 恒成立,所以
恒成立,所以 ……15分
……15分
考点:本小题主要考查轨迹方程的求法、直线与椭圆的位置关系、向量的运算和恒成立问题,考查学生运算求解的基本技能、推理论证能力和数形结合思想.
点评:这是一道直线与圆锥曲线的综合题目,求轨迹方程时,不要忘记限制条件;设直线方程时,不要忘记考虑斜率存在与不存在两种可能,总之思路一定要细致,解题步骤一定要严谨.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 .
. 在
在 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数 的最大值;
的最大值; 对任意的
对任意的 ,
, 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. 为自然对数的底数.
为自然对数的底数. 与曲线
与曲线 相切
相切 在
在 上恰有两个不等的实数根
上恰有两个不等的实数根 ,求
,求 的大小
的大小 :
: (
( ),焦点为
),焦点为 ,直线
,直线 交抛物线
交抛物线 、
、 两点,
两点, 是线段
是线段 的中点,
的中点, 轴的垂线交抛物线
轴的垂线交抛物线 ,
, 到焦点
到焦点 ,求此时
,求此时 的值;
的值; 是以
是以

 的单调区间;
的单调区间; ,若
,若 在
在 上不单调且仅在
上不单调且仅在 处取得最大值,求
处取得最大值,求 的取值范围.
的取值范围.